Chào mừng bạn đến với bài học về Lý thuyết Thứ tự thực hiện các phép tính. Quy tắc dấu ngoặc, một trong những kiến thức cơ bản và quan trọng nhất của chương trình Toán 7 - Kết nối tri thức. Việc nắm vững quy tắc này sẽ giúp bạn giải quyết các bài toán một cách chính xác và hiệu quả.
Bài học này sẽ cung cấp cho bạn những kiến thức chi tiết về thứ tự ưu tiên của các phép tính, cách sử dụng dấu ngoặc để thay đổi thứ tự thực hiện phép tính, cùng với các ví dụ minh họa cụ thể.
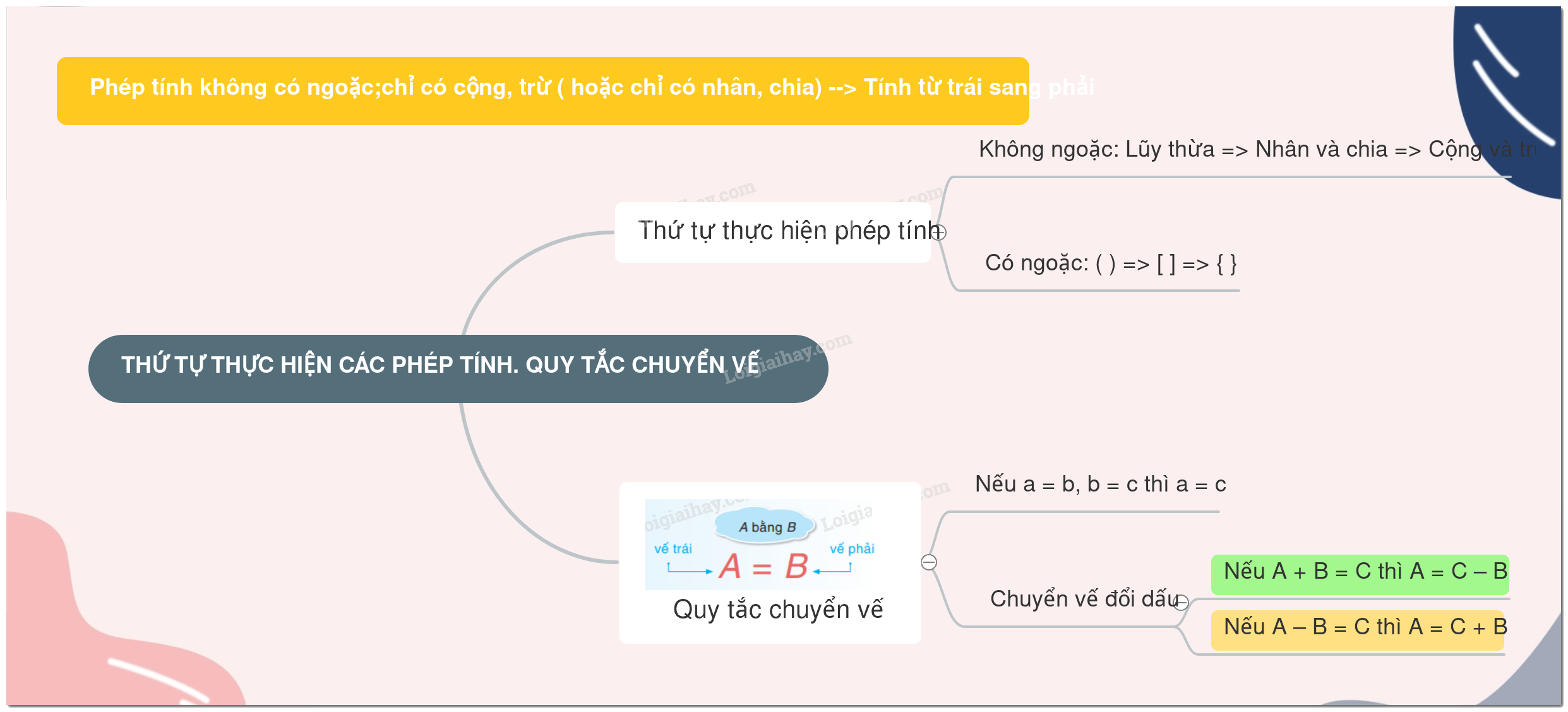
1. Thứ tự thực hiện các phép tính
1. Thứ tự thực hiện các phép tính
* Với các biểu thức chỉ có phép cộng và phép trừ hoặc chỉ có phép nhân và phép chia, ta thực hiện các phép tính từ trái sang phải.
* Với các biểu thức không có dấu ngoặc, ta thực hiện theo thứ tự:
Lũy thừa => Nhân và chia => Cộng và trừ
* Với các biểu thức có dấu ngoặc, ta thực hiện trong ngoặc trước, ngoài ngoặc sau. Trường hợp có nhiều dấu ngoặc, ta thực hiện theo thứ tự ( ) => [ ] => { }
2. Quy tắc chuyển vế
Đẳng thức:
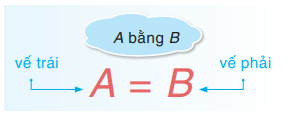
Nếu a = b thì b = a ; a + c = b + c
Quy tắc chuyển vế:
Khi chuyển một số hạng từ vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng đó: dấu “ +” đổi thành dấu “ – “; dấu “ – “ đổi thành dấu “ +”.
+) Nếu A + B = C thì A = C – B
+) Nếu A – B = C thì A = C + B
Ví dụ: 3x – 2 = x – 6
\( \Leftrightarrow \)3x – x = - 6 + 2
\( \Leftrightarrow \)2x = -4
\( \Leftrightarrow \)x = (-4) : 2
\( \Leftrightarrow \)x = -2
Vậy x = -2
Trong toán học, thứ tự thực hiện các phép tính là một quy tắc quan trọng để đảm bảo tính chính xác của kết quả. Quy tắc này được áp dụng cho tất cả các phép tính, từ đơn giản đến phức tạp. Hiểu rõ quy tắc này là nền tảng để giải quyết các bài toán đại số và hình học ở các lớp học cao hơn.
Thứ tự thực hiện các phép tính được quy định như sau:
Để dễ nhớ, chúng ta có thể sử dụng câu khẩu hiệu: “Ngoặc, lũy thừa, nhân chia, cộng trừ”.
Dấu ngoặc được sử dụng để thay đổi thứ tự thực hiện các phép tính. Các phép tính trong dấu ngoặc luôn được thực hiện trước các phép tính bên ngoài dấu ngoặc.
Có ba loại dấu ngoặc thường gặp:
Khi có nhiều loại dấu ngoặc khác nhau trong một biểu thức, chúng ta thực hiện các phép tính theo thứ tự sau: ngoặc nhọn, ngoặc vuông, ngoặc đơn.
Hãy xem xét các ví dụ sau để hiểu rõ hơn về cách áp dụng quy tắc thứ tự thực hiện các phép tính:
Áp dụng quy tắc, ta thực hiện phép nhân trước:
2 + 3 × 4 = 2 + 12 = 14
Áp dụng quy tắc, ta thực hiện phép tính trong dấu ngoặc trước:
(2 + 3) × 4 = 5 × 4 = 20
Áp dụng quy tắc, ta thực hiện phép lũy thừa trước, sau đó đến phép trừ và cộng:
10 - 22 + 4 = 10 - 4 + 4 = 10
Để củng cố kiến thức, hãy thử giải các bài tập sau:
Khi thực hiện các phép tính, hãy luôn tuân thủ đúng quy tắc thứ tự thực hiện các phép tính. Điều này sẽ giúp bạn tránh được những sai sót không đáng có và đảm bảo tính chính xác của kết quả.
Ngoài ra, hãy chú ý đến việc sử dụng dấu ngoặc một cách hợp lý để thay đổi thứ tự thực hiện các phép tính khi cần thiết.
Lý thuyết Thứ tự thực hiện các phép tính. Quy tắc dấu ngoặc là một kiến thức cơ bản và quan trọng trong toán học. Việc nắm vững kiến thức này sẽ giúp bạn giải quyết các bài toán một cách dễ dàng và hiệu quả. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán của mình.
| Phép tính | Thứ tự thực hiện |
|---|---|
| Dấu ngoặc | Thực hiện trước |
| Lũy thừa | Thực hiện sau dấu ngoặc |
| Nhân và Chia | Thực hiện từ trái sang phải |
| Cộng và Trừ | Thực hiện từ trái sang phải |