Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 7. Bài viết này sẽ hướng dẫn bạn giải quyết các bài tập trong mục 3 trang 18 sách giáo khoa Toán 7 tập 1 - Kết nối tri thức một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc học Toán đôi khi có thể gặp nhiều khó khăn. Vì vậy, chúng tôi luôn cố gắng cung cấp những giải pháp tốt nhất, giúp bạn nắm vững kiến thức và tự tin hơn trong học tập.
Viết số 2^2^3 dưới dạng lũy thừa cơ số 2 ....Viết các số ...Cho hình vuông như Hình 1.12. Em hãy thay mỗi dấu “?” bằng một lũy thừa của 2, biết các lũy thừa trên mỗi hàng, mỗi cột và mỗi đường chéo đều bằng nhau.
Viết các số \({\left( {\frac{1}{4}} \right)^8};{\left( {\frac{1}{8}} \right)^3}\) dưới dạng lũy thừa cơ số \(\frac{1}{2}\)
Phương pháp giải:
+ Bước 1: Viết các số \(\frac{1}{4};\frac{1}{8}\) dưới dạng lũy thừa cơ số \(\frac{1}{2}\)
+ Bước 2: Sử dụng công thức lũy thừa của lũy thừa: \({({x^m})^n} = {x^{m.n}}\)
Lời giải chi tiết:
Ta có:
\(\begin{array}{l}{\left( {\frac{1}{4}} \right)^8} = {[{\left( {\frac{1}{2}} \right)^2}]^8} = {(\frac{1}{2})^{2.8}} = {(\frac{1}{2})^{16}};\\{\left( {\frac{1}{8}} \right)^3} = {[{(\frac{1}{2})^3}]^3} = {(\frac{1}{2})^{3.3}} = {(\frac{1}{2})^9}\end{array}\)
Viết số \({({2^2})^3}\) dưới dạng lũy thừa cơ số 2 và số \({\left[ {{{( - 3)}^2}} \right]^2}\) dưới dạng lũy thừa cơ số \(-3\).
Phương pháp giải:
Sử dụng định nghĩa lũy thừa và công thức tích các lũy thừa có cùng cơ số
Lời giải chi tiết:
Ta có: +) \({({2^2})^3} = {2^2}{.2^2}{.2^2} = {2^{2 + 2 + 2}} = {2^6}\)
+) \({\left[ {{{( - 3)}^2}} \right]^2} = {( - 3)^2}.{( - 3)^2} = {( - 3)^{2 + 2}} = {( - 3)^4}\)
Viết số \({({2^2})^3}\) dưới dạng lũy thừa cơ số 2 và số \({\left[ {{{( - 3)}^2}} \right]^2}\) dưới dạng lũy thừa cơ số \(-3\).
Phương pháp giải:
Sử dụng định nghĩa lũy thừa và công thức tích các lũy thừa có cùng cơ số
Lời giải chi tiết:
Ta có: +) \({({2^2})^3} = {2^2}{.2^2}{.2^2} = {2^{2 + 2 + 2}} = {2^6}\)
+) \({\left[ {{{( - 3)}^2}} \right]^2} = {( - 3)^2}.{( - 3)^2} = {( - 3)^{2 + 2}} = {( - 3)^4}\)
Viết các số \({\left( {\frac{1}{4}} \right)^8};{\left( {\frac{1}{8}} \right)^3}\) dưới dạng lũy thừa cơ số \(\frac{1}{2}\)
Phương pháp giải:
+ Bước 1: Viết các số \(\frac{1}{4};\frac{1}{8}\) dưới dạng lũy thừa cơ số \(\frac{1}{2}\)
+ Bước 2: Sử dụng công thức lũy thừa của lũy thừa: \({({x^m})^n} = {x^{m.n}}\)
Lời giải chi tiết:
Ta có:
\(\begin{array}{l}{\left( {\frac{1}{4}} \right)^8} = {[{\left( {\frac{1}{2}} \right)^2}]^8} = {(\frac{1}{2})^{2.8}} = {(\frac{1}{2})^{16}};\\{\left( {\frac{1}{8}} \right)^3} = {[{(\frac{1}{2})^3}]^3} = {(\frac{1}{2})^{3.3}} = {(\frac{1}{2})^9}\end{array}\)
Cho hình vuông như Hình 1.12. Em hãy thay mỗi dấu “?” bằng một lũy thừa của 2, biết các lũy thừa trên mỗi hàng, mỗi cột và mỗi đường chéo đều bằng nhau.
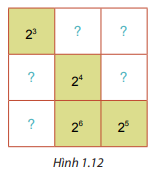
Phương pháp giải:
Tính tích của 3 ô in đậm ở đường chéo đã biết. Tích này chính là tích của từng hàng , cột.
Tính hàng, cột khi biết tích của hàng, cột và 2 ô của hàng, cột đó.
Lời giải chi tiết:
Ta đặt các ô chưa biết như sau:
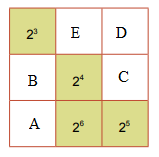
Ta có:
Tích của mỗi hàng, cột, đường chéo bằng: \({2^3}{.2^4}{.2^5} = {2^{3 + 4 + 5}} = {2^{12}}\)
\(\begin{array}{l}A = {2^{12}}:{2^6}:{2^5} = {2^{12 - 6 - 5}} = {2^1} = 2;\\B = {2^{12}}:{2^1}:{2^3} = {2^{12 - 1 - 3}} = {2^8};\\C = {2^{12}}:{2^8}:{2^4} = {2^{12 - 8 - 4}} = {2^0} = 1;\\D = {2^{12}}:{2^0}:{2^5} = {2^{12 - 0 - 5}} = {2^7};\\E = {2^{12}}:{2^7}:{2^3} = {2^{12 - 7 - 3}} = {2^2}\end{array}\)
Vậy ta có bảng hoàn chỉnh là:
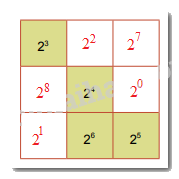
Cho hình vuông như Hình 1.12. Em hãy thay mỗi dấu “?” bằng một lũy thừa của 2, biết các lũy thừa trên mỗi hàng, mỗi cột và mỗi đường chéo đều bằng nhau.
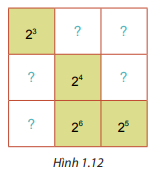
Phương pháp giải:
Tính tích của 3 ô in đậm ở đường chéo đã biết. Tích này chính là tích của từng hàng , cột.
Tính hàng, cột khi biết tích của hàng, cột và 2 ô của hàng, cột đó.
Lời giải chi tiết:
Ta đặt các ô chưa biết như sau:
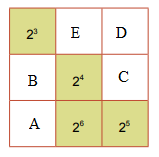
Ta có:
Tích của mỗi hàng, cột, đường chéo bằng: \({2^3}{.2^4}{.2^5} = {2^{3 + 4 + 5}} = {2^{12}}\)
\(\begin{array}{l}A = {2^{12}}:{2^6}:{2^5} = {2^{12 - 6 - 5}} = {2^1} = 2;\\B = {2^{12}}:{2^1}:{2^3} = {2^{12 - 1 - 3}} = {2^8};\\C = {2^{12}}:{2^8}:{2^4} = {2^{12 - 8 - 4}} = {2^0} = 1;\\D = {2^{12}}:{2^0}:{2^5} = {2^{12 - 0 - 5}} = {2^7};\\E = {2^{12}}:{2^7}:{2^3} = {2^{12 - 7 - 3}} = {2^2}\end{array}\)
Vậy ta có bảng hoàn chỉnh là:
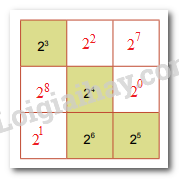
Mục 3 trang 18 SGK Toán 7 tập 1 - Kết nối tri thức thường xoay quanh các bài tập về số nguyên, phép cộng, trừ, nhân, chia số nguyên, và các tính chất của các phép toán này. Việc nắm vững kiến thức cơ bản về số nguyên là nền tảng quan trọng để học tốt các chương trình Toán học tiếp theo.
Mục 3 thường bao gồm các bài tập với mức độ khó tăng dần, từ việc thực hiện các phép tính đơn giản đến việc áp dụng các tính chất để giải quyết các bài toán phức tạp hơn. Dưới đây là phân tích chi tiết từng bài tập:
Bài 1 thường yêu cầu học sinh thực hiện các phép cộng, trừ, nhân, chia số nguyên. Để giải bài tập này, học sinh cần nắm vững quy tắc cộng, trừ, nhân, chia số nguyên. Ví dụ:
Bài 2 yêu cầu học sinh tìm số thích hợp để điền vào chỗ trống, sao cho biểu thức trở nên đúng. Để giải bài tập này, học sinh cần áp dụng các tính chất của các phép toán và sử dụng các phép toán ngược để tìm ra số cần điền.
Ví dụ: x + 5 = 2 => x = 2 - 5 = -3
Bài 3 thường là các bài toán có liên quan đến thực tế, yêu cầu học sinh áp dụng kiến thức về số nguyên để giải quyết các vấn đề trong cuộc sống. Ví dụ: Một người nông dân bị lỗ 500.000 đồng trong vụ mùa vừa qua. Hỏi người nông dân đó còn lại bao nhiêu tiền nếu trước đó người đó có 2.000.000 đồng?
Giải: 2.000.000 - 500.000 = 1.500.000 đồng
Bài tập: Tính giá trị của biểu thức: (-3) * 4 + 5 * (-2) - 10
Giải:
Vậy giá trị của biểu thức là -32.
Để học tốt môn Toán 7, bạn có thể tham khảo thêm các tài liệu sau:
Hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức và kỹ năng cần thiết để giải quyết các bài tập trong mục 3 trang 18 SGK Toán 7 tập 1 - Kết nối tri thức một cách hiệu quả. Chúc bạn học tốt!