Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 7 tập 2 của giaitoan.edu.vn. Ở đây, chúng tôi cung cấp lời giải chi tiết và dễ hiểu cho tất cả các bài tập trong sách giáo khoa Toán 7 tập 2 - Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em học sinh nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
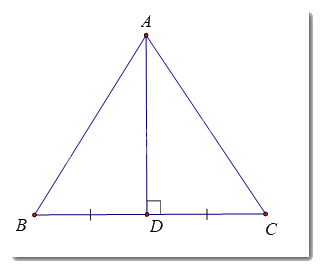
Vẽ tam giác ABC và 3 đường cao của nó. Quan sát hình và cho biết, ba đường cao đó có cùng đi qua một điểm hay không ?
Mỗi tam giác có mấy đường cao?
Phương pháp giải:
Đường cao là đoạn thẳng đi qua đỉnh và vuông góc với cạnh đối diện.
Lời giải chi tiết:
Ứng với 1 cạnh của tam giác, ta có 1 đường cao
Vậy mỗi tam giác có 3 đường cao.
Vẽ tam giác ABC và 3 đường cao của nó. Quan sát hình và cho biết, ba đường cao đó có cùng đi qua một điểm hay không ?
Phương pháp giải:
Đường cao của một tam giác là đoạn thẳng kẻ từ một đỉnh và vuông góc với cạnh đối diện
Lời giải chi tiết:
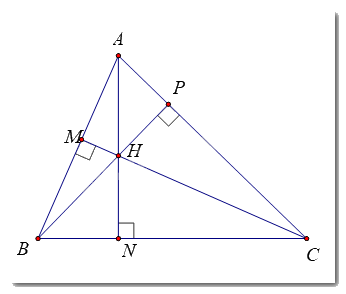
Ba đường cao AN, BP, CM cùng đi qua điểm H.
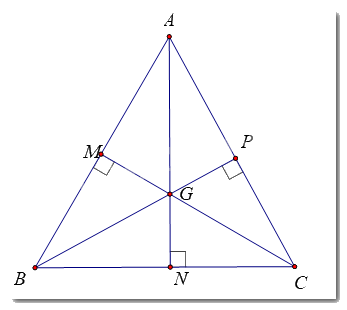
a) Chứng minh trong tam giác ABC cân tại A, đường trung trực của cạnh BC là đường cao và cũng là đường phân giác xuất phát từ đỉnh A của tam giác đó.
b) Chứng minh rằng trong tam giác đều, điểm cách đều ba đỉnh cũng cách đều ba cạnh của tam giác.
Phương pháp giải:
a) Chứng minh A thuộc đường trung trực BC nên AD là đường cao.
Chứng minh: \(\Delta ABD = \Delta ACD\) từ đó suy ra AD là phân giác góc A
b) Điểm cách đều ba đỉnh là giao của ba đường trung trực trong tam giác GA = GB = GC
Sử dụng kết quả ý a, chứng minh G là giao điểm ba đường phân giác trong tam giác ABC
Lời giải chi tiết:
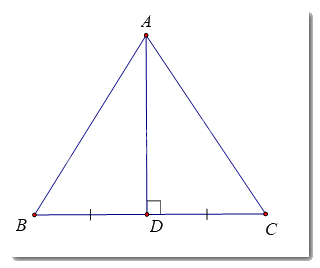
a) Kẻ đường trung trực của đoạn thẳng BC, cắt BC tại D
Ta có: Tam giác ABC cân nên AB = AC
\( \Rightarrow A\)thuộc đường trung trực của cạnh BC (t/c)
\( \Rightarrow AD\)là đường trung trực của BC.
Xét \(\Delta ABD\)và \(\Delta ACD\)có:
AB = AC (gt)
BD = CD (gt)
AD: cạnh chung
\( \Rightarrow \Delta ABD = \Delta ACD\left( {c - c - c} \right)\)
\( \Rightarrow \widehat {BAD} = \widehat {CAD}\)
\( \Rightarrow \)AD là tia phân giác góc BAC. Vậy tam giác ABC cân tại A, đường trung trực của cạnh BC là đường cao và cũng là đường phân giác xuất phát từ đỉnh A của tam giác đó.
b)
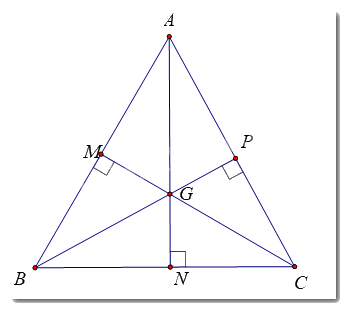
Ta có: Điểm cách đều ba đỉnh của tam giác là giao điểm ba đường trung trực của tam giác đó.
Tam giác ABC đều nên AB = BC = CA
Tam giác ABC cân tại A có AN là đường trung tuyến
\( \Rightarrow \) AN là đường phân giác xuất phát từ đỉnh A (cm ở ý a)
Tương tự: BP, CM lần lượt là đường phân giác xuất phát từ B và C của tam giác ABC
Mà AN cắt BP tại G
\( \Rightarrow G\) là giao điểm ba đường phân giác của tam giác ABC
\( \Rightarrow G\) cách đều ba cạnh của tam giác ABC (Tính chất)
Mỗi tam giác có mấy đường cao?
Phương pháp giải:
Đường cao là đoạn thẳng đi qua đỉnh và vuông góc với cạnh đối diện.
Lời giải chi tiết:
Ứng với 1 cạnh của tam giác, ta có 1 đường cao
Vậy mỗi tam giác có 3 đường cao.
Vẽ tam giác ABC và 3 đường cao của nó. Quan sát hình và cho biết, ba đường cao đó có cùng đi qua một điểm hay không ?
Phương pháp giải:
Đường cao của một tam giác là đoạn thẳng kẻ từ một đỉnh và vuông góc với cạnh đối diện
Lời giải chi tiết:
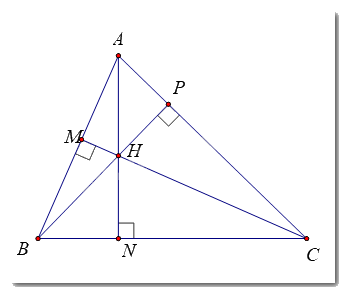
Ba đường cao AN, BP, CM cùng đi qua điểm H.
a) Chứng minh trong tam giác ABC cân tại A, đường trung trực của cạnh BC là đường cao và cũng là đường phân giác xuất phát từ đỉnh A của tam giác đó.
b) Chứng minh rằng trong tam giác đều, điểm cách đều ba đỉnh cũng cách đều ba cạnh của tam giác.
Phương pháp giải:
a) Chứng minh A thuộc đường trung trực BC nên AD là đường cao.
Chứng minh: \(\Delta ABD = \Delta ACD\) từ đó suy ra AD là phân giác góc A
b) Điểm cách đều ba đỉnh là giao của ba đường trung trực trong tam giác GA = GB = GC
Sử dụng kết quả ý a, chứng minh G là giao điểm ba đường phân giác trong tam giác ABC
Lời giải chi tiết:
a) Kẻ đường trung trực của đoạn thẳng BC, cắt BC tại D
Ta có: Tam giác ABC cân nên AB = AC
\( \Rightarrow A\)thuộc đường trung trực của cạnh BC (t/c)
\( \Rightarrow AD\)là đường trung trực của BC.
Xét \(\Delta ABD\)và \(\Delta ACD\)có:
AB = AC (gt)
BD = CD (gt)
AD: cạnh chung
\( \Rightarrow \Delta ABD = \Delta ACD\left( {c - c - c} \right)\)
\( \Rightarrow \widehat {BAD} = \widehat {CAD}\)
\( \Rightarrow \)AD là tia phân giác góc BAC. Vậy tam giác ABC cân tại A, đường trung trực của cạnh BC là đường cao và cũng là đường phân giác xuất phát từ đỉnh A của tam giác đó.
b)
Ta có: Điểm cách đều ba đỉnh của tam giác là giao điểm ba đường trung trực của tam giác đó.
Tam giác ABC đều nên AB = BC = CA
Tam giác ABC cân tại A có AN là đường trung tuyến
\( \Rightarrow \) AN là đường phân giác xuất phát từ đỉnh A (cm ở ý a)
Tương tự: BP, CM lần lượt là đường phân giác xuất phát từ B và C của tam giác ABC
Mà AN cắt BP tại G
\( \Rightarrow G\) là giao điểm ba đường phân giác của tam giác ABC
\( \Rightarrow G\) cách đều ba cạnh của tam giác ABC (Tính chất)
Mục 2 của chương trình Toán 7 tập 2 - Kết nối tri thức tập trung vào việc ôn tập và củng cố các kiến thức về biểu thức đại số, đa thức, và các phép toán trên đa thức. Các bài tập trong mục này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện tư duy logic và khả năng tính toán.
Các bài tập trang 79 chủ yếu tập trung vào việc nhận biết và phân loại các biểu thức đại số, đa thức. Học sinh cần nắm vững các khái niệm về biến, số, hệ số, bậc của đa thức để giải quyết các bài tập này.
Trang 80 tập trung vào các phép toán cộng, trừ, nhân đa thức. Học sinh cần nắm vững các quy tắc cộng, trừ, nhân đa thức để thực hiện các phép toán này một cách chính xác.
Trang 81 là phần vận dụng các kiến thức đã học để giải các bài toán thực tế. Các bài toán này thường có tính ứng dụng cao, giúp học sinh hiểu rõ hơn về tầm quan trọng của Toán học trong cuộc sống.
Bài 6: Một khu vườn hình chữ nhật có chiều dài là 2x + 3 (m) và chiều rộng là x - 1 (m). Tính chu vi và diện tích của khu vườn này. (Giải thích chi tiết cách giải bài toán)
Để giải các bài tập trong mục 2 này một cách hiệu quả, học sinh cần:
Toán 7 là một môn học quan trọng, là nền tảng cho các môn học tiếp theo. Để học tốt Toán 7, học sinh cần:
Hy vọng với lời giải chi tiết và các phương pháp giải bài tập hiệu quả mà giaitoan.edu.vn cung cấp, các em học sinh sẽ tự tin hơn khi giải các bài tập trong mục 2 trang 79, 80, 81 SGK Toán 7 tập 2 - Kết nối tri thức. Chúc các em học tập tốt!