Bài 10.7 trang 93 SGK Toán 7 tập 2 thuộc chương trình Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về các góc tạo bởi đường thẳng cắt đường thẳng. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các vấn đề thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 10.7 trang 93 SGK Toán 7 tập 2, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
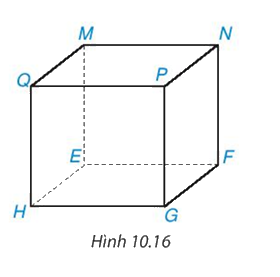
Kể tên các đỉnh, cạnh và đường chéo của hình lập phương MNPQ. EFGH ở Hình 10.16.
Đề bài
Kể tên các đỉnh, cạnh và đường chéo của hình lập phương MNPQ. EFGH ở Hình 10.16.
Phương pháp giải - Xem chi tiết
Xem lại các hoạt động 2, 3 bài 36
Lời giải chi tiết
Ta có
+ 8 đỉnh :M, Q, P, N, H, E, F, G.
+ 12 cạnh : MQ, MN, QP, PN, HE, EF, FG, GH, QH, ME, NF, PG.
+ 4 đường chéo : MG, EP, QF, HN
Bài 10.7 trang 93 SGK Toán 7 tập 2 yêu cầu chúng ta giải quyết một bài toán thực tế liên quan đến các góc tạo bởi đường thẳng cắt đường thẳng. Để giải bài toán này, chúng ta cần nắm vững các kiến thức sau:
Nội dung bài toán: (Giả sử bài toán có nội dung cụ thể về một hình vẽ và yêu cầu tính góc. Phần này cần được thay thế bằng nội dung bài toán thực tế)
Ví dụ, bài toán có thể yêu cầu:
Cho hình vẽ, biết góc A = 60 độ. Tính góc B.
Lời giải:
Ví dụ cụ thể:
Nếu góc A và góc B là hai góc so le trong, thì góc B = góc A = 60 độ.
Nếu góc A và góc B là hai góc kề bù, thì góc B = 180 độ - góc A = 180 độ - 60 độ = 120 độ.
Lưu ý:
Để củng cố kiến thức về các góc tạo bởi đường thẳng cắt đường thẳng, các em có thể làm thêm các bài tập sau:
Bài 10.7 trang 93 SGK Toán 7 tập 2 là một bài tập quan trọng giúp học sinh hiểu rõ và vận dụng các kiến thức về các góc tạo bởi đường thẳng cắt đường thẳng. Hy vọng với lời giải chi tiết và hướng dẫn cụ thể của Giaitoan.edu.vn, các em học sinh sẽ tự tin giải quyết bài toán này và đạt kết quả tốt trong môn Toán.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!
| Góc | Định nghĩa | Tính chất |
|---|---|---|
| So le trong | Nằm bên trong hai đường thẳng và ở hai phía đối diện của đường thẳng cắt | Bằng nhau nếu hai đường thẳng song song |
| So le ngoài | Nằm bên ngoài hai đường thẳng và ở hai phía đối diện của đường thẳng cắt | Bằng nhau nếu hai đường thẳng song song |
| Đồng vị | Nằm cùng phía của đường thẳng cắt và ở cùng một phía của hai đường thẳng | Bằng nhau nếu hai đường thẳng song song |