Chào mừng bạn đến với bài học về Lý thuyết Tỉ lệ thức Toán 7 - Kết nối tri thức tại giaitoan.edu.vn. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về tỉ lệ thức, giúp bạn giải quyết các bài toán một cách dễ dàng và hiệu quả.
Chúng tôi sẽ trình bày lý thuyết một cách rõ ràng, dễ hiểu, kèm theo các ví dụ minh họa cụ thể. Ngoài ra, bạn sẽ được luyện tập với các bài tập đa dạng để củng cố kiến thức đã học.
Định nghĩa tỉ lệ thức
I. Các kiến thức cần nhớ
Định nghĩa tỉ lệ thức
+ Tỉ lệ thức là đẳng thức của hai tỉ số \(\dfrac{a}{b} = \dfrac{c}{d}\)
+ Tỉ lệ thức \(\dfrac{a}{b} = \dfrac{c}{d}\) còn được viết là \(a:b = c:d\)
Ví dụ: \(\dfrac{{28}}{{24}} = \dfrac{7}{6};\)\(\dfrac{3}{{10}} = \dfrac{{2,1}}{7}\)
Tính chất tỉ lệ thức
+ Tính chất 1 (tính chất cơ bản của tỉ lệ thức)
Nếu \(\dfrac{a}{b} = \dfrac{c}{d}\) thì \(a.d = b.c\)
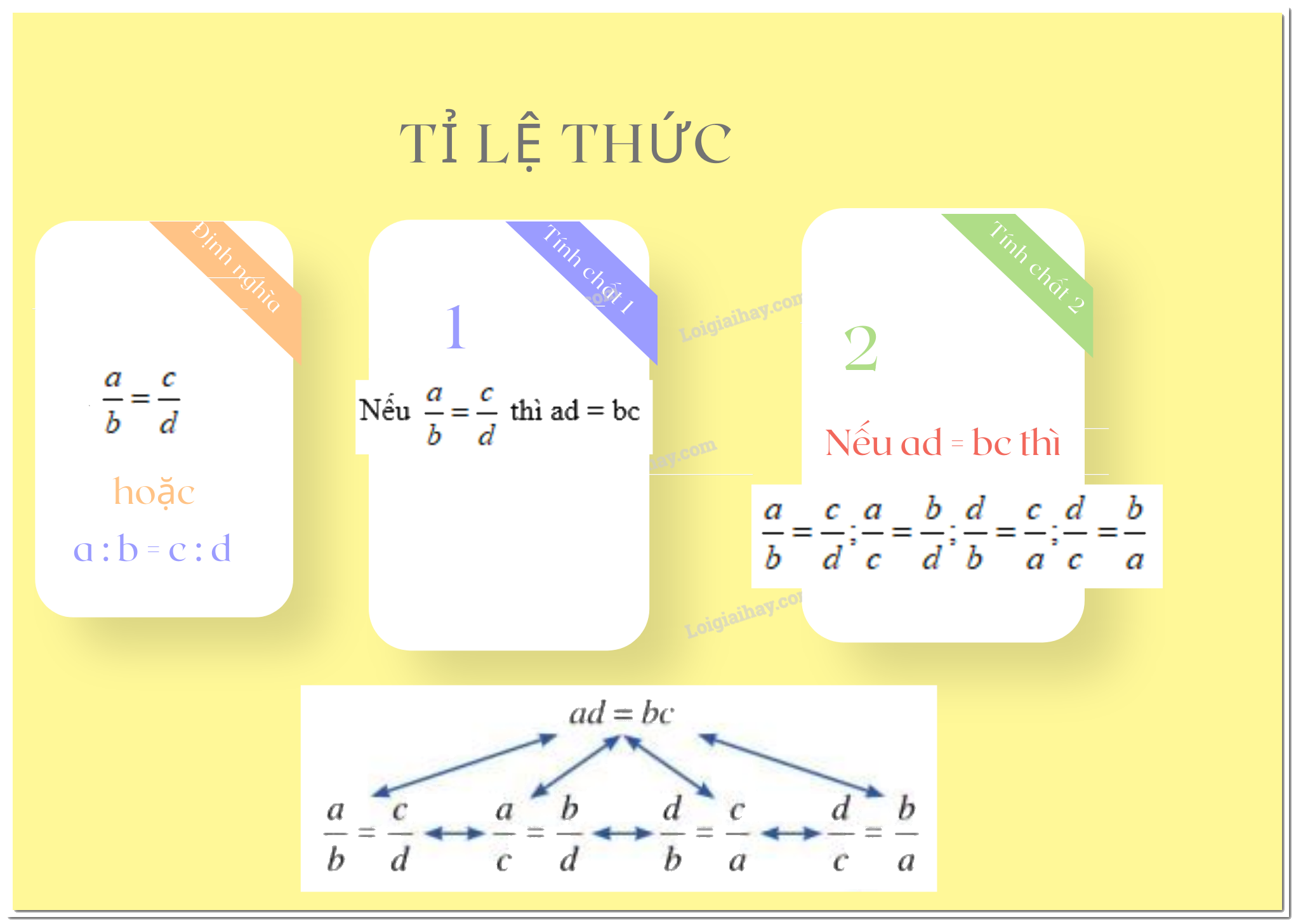
+ Tính chất 2 (điều kiện để bốn số lập thành tỉ lệ thức): Nếu \(ad=bc\) và \(a,b,c,d \ne 0\) thì ta có các tỉ lệ thức
\(\dfrac{a}{b} = \dfrac{c}{d}\); \(\dfrac{a}{c} = \dfrac{b}{d}\); \(\dfrac{d}{b} = \dfrac{c}{a};\) \(\dfrac{d}{c} = \dfrac{b}{a}.\)
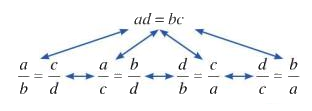
Ví dụ: Ta có \(\dfrac{3}{6} = \dfrac{9}{{18}} \Rightarrow 3.18 = 9.6\left( { = 54} \right)\)
Vì \(4.9 = 3.12(=36)\) nên ta có các tỉ lệ thức sau: \(\dfrac{4}{3} = \dfrac{{12}}{9};\,\dfrac{3}{4} = \dfrac{9}{{12}};\dfrac{4}{{12}} = \dfrac{3}{9};\dfrac{{12}}{4} = \dfrac{9}{3}\)
II. Các dạng toán thường gặp
Dạng 1: Lập tỉ lệ thức từ đẳng thức cho trước
Phương pháp:
Ta sử dụng: Nếu \(a.d = b.c\) thì
\(\dfrac{a}{b} = \dfrac{c}{d}\); \(\dfrac{a}{c} = \dfrac{b}{d}\); \(\dfrac{d}{b} = \dfrac{c}{a};\) \(\dfrac{d}{c} = \dfrac{b}{a}.\)
Dạng 2: Tìm x, y
Phương pháp:
Sử dụng tính chất cơ bản của tỉ lệ thức: Nếu \(\dfrac{a}{b} = \dfrac{c}{d}\) thì \(a.d = b.c\)
Trong một tỉ lệ thức ta có thể tìm một số hạng chưa biết khi biết ba số hạng còn lại.
\(\dfrac{a}{b} = \dfrac{c}{d} \Rightarrow a = \dfrac{{bc}}{d};\,b = \dfrac{{ad}}{c};\)\(c = \dfrac{{ad}}{b};\,d = \dfrac{{bc}}{a}\) .
Ví dụ: Tìm x biết \(\dfrac{x}{2} = \dfrac{8}{6}\)
Ta có:
\(\begin{array}{l}\dfrac{x}{2} = \dfrac{8}{6}\\\Rightarrow x.6 = 8.2\\\Rightarrow x = \dfrac{{16}}{6}\\\Rightarrow x = \dfrac{8}{3}\end{array}\)
Dạng 3: Chứng minh các tỉ lệ thức
Phương pháp:
Dựa vào các tính chất của tỉ lệ thức và biến đổi linh hoạt để chứng minh.
Tỉ lệ thức là một khái niệm quan trọng trong chương trình Toán 7, Kết nối tri thức. Hiểu rõ về tỉ lệ thức sẽ giúp học sinh giải quyết nhiều bài toán thực tế và là nền tảng cho các kiến thức toán học nâng cao hơn.
Tỉ lệ thức là sự bằng nhau của hai tỉ số. Nói cách khác, nếu ta có bốn số a, b, c, d khác 0, thì a/b = c/d được gọi là một tỉ lệ thức. Trong đó:
Tính chất cơ bản của tỉ lệ thức là:
Nếu a/b = c/d thì ad = bc
Tính chất này được sử dụng rộng rãi trong việc chứng minh và giải các bài toán liên quan đến tỉ lệ thức.
Có nhiều dạng bài tập về tỉ lệ thức, bao gồm:
Ví dụ 1: Kiểm tra xem 2/3 và 4/6 có lập thành tỉ lệ thức hay không?
Ta có: 2 * 6 = 12 và 3 * 4 = 12. Vì 12 = 12 nên 2/3 và 4/6 lập thành tỉ lệ thức.
Ví dụ 2: Tìm x trong tỉ lệ thức 3/x = 6/8
Áp dụng tính chất ad = bc, ta có: 3 * 8 = x * 6 => 24 = 6x => x = 4
Tỉ lệ thức không chỉ xuất hiện trong các bài toán toán học mà còn được ứng dụng rộng rãi trong đời sống thực tế. Ví dụ:
Để nắm vững kiến thức về tỉ lệ thức, bạn nên luyện tập thêm với các bài tập khác nhau. Giaitoan.edu.vn cung cấp một hệ thống bài tập đa dạng và phong phú, giúp bạn củng cố kiến thức và rèn luyện kỹ năng giải toán.
Lý thuyết Tỉ lệ thức Toán 7 - Kết nối tri thức là một phần quan trọng của chương trình học. Việc hiểu rõ định nghĩa, tính chất và các dạng bài tập về tỉ lệ thức sẽ giúp bạn tự tin hơn trong việc giải toán và ứng dụng kiến thức vào thực tế.
Chúc bạn học tốt và đạt kết quả cao trong môn Toán!