Chào mừng các em học sinh lớp 7 đến với bài học về Lý thuyết Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất trong chương trình Toán 7 Kết nối tri thức. Bài học này sẽ cung cấp cho các em những kiến thức cơ bản và quan trọng nhất về việc xác định hai tam giác bằng nhau dựa trên các yếu tố tương ứng.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, các yếu tố cần thiết để chứng minh hai tam giác bằng nhau, và đặc biệt là trường hợp bằng nhau thứ nhất (cạnh - góc - cạnh). Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
1. Hai tam giác bằng nhau
1. Hai tam giác bằng nhau
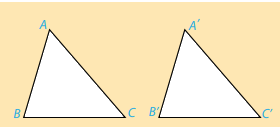
Hai tam giác ABC và A’B’C’ bằng nhau nếu chúng có các cạnh tương ứng bằng nhau và các góc tương ứng bằng nhau, tức là:
AB = A’B’ ; AC = A’C’ ; BC = B’C’ và \(\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\)
Ta viết: \(\Delta ABC = \Delta A'B'C'\)
Nếu 2 tam giác bằng nhau, ta suy ra tất cả các cạnh, các góc tương ứng bằng nhau.
2. Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh (c.c.c)
Nếu 3 cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
Ví dụ:
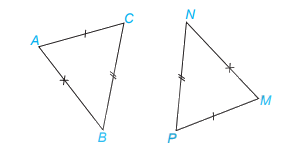
Xét \(\Delta ABC\) và \(\Delta MNP\) có:
\(\begin{array}{l}AB = MN\\BC = NP\\AC = MP\end{array}\)
Vậy\(\Delta ABC\) =\(\Delta MNP\)(c.c.c)
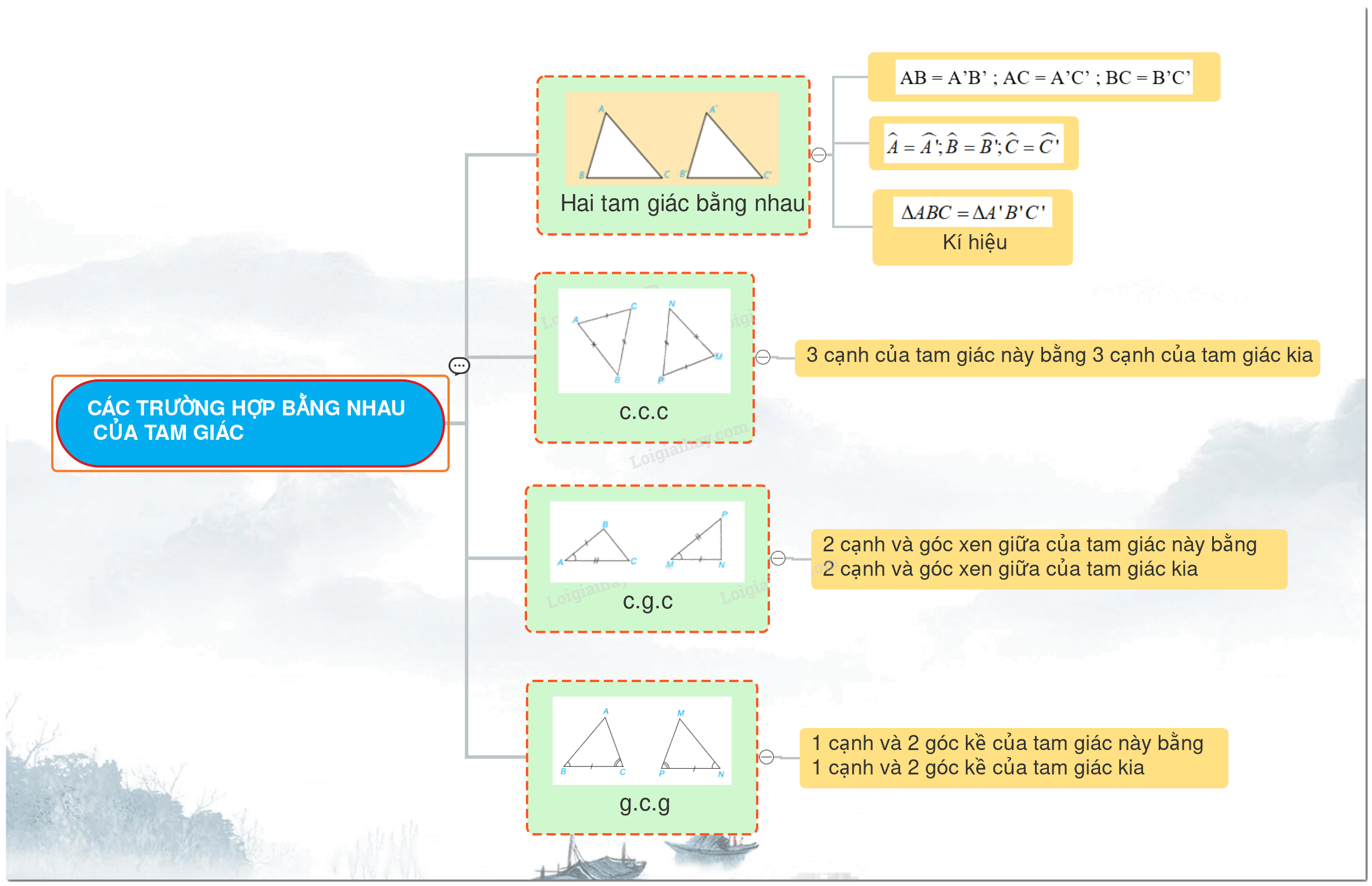
Trong hình học, việc xác định sự bằng nhau của các hình là một vấn đề quan trọng. Đối với tam giác, có nhiều cách để chứng minh hai tam giác bằng nhau. Bài viết này sẽ tập trung vào lý thuyết hai tam giác bằng nhau và đặc biệt là trường hợp bằng nhau thứ nhất (cạnh - góc - cạnh) trong chương trình Toán 7 Kết nối tri thức.
Hai tam giác được gọi là bằng nhau nếu chúng có các cạnh tương ứng bằng nhau và các góc tương ứng bằng nhau. Điều này có nghĩa là nếu tam giác ABC và tam giác A'B'C' bằng nhau, thì:
Để chứng minh hai tam giác bằng nhau, chúng ta không cần phải chứng minh tất cả các cạnh và góc tương ứng bằng nhau. Thay vào đó, chúng ta có thể sử dụng các trường hợp bằng nhau của tam giác. Có ba trường hợp bằng nhau thường được sử dụng:
Phát biểu: Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
Ký hiệu: Nếu AB = A'B', ∠A = ∠A', và AC = A'C' thì ΔABC = ΔA'B'C'.
Ví dụ 1: Cho tam giác ABC và tam giác DEF có AB = DE, ∠A = ∠D, và AC = DF. Chứng minh rằng ΔABC = ΔDEF.
Giải:
Xét ΔABC và ΔDEF, ta có:
Vậy, ΔABC = ΔDEF (trường hợp bằng nhau cạnh - góc - cạnh).
Ví dụ 2: Cho hình vẽ, biết AB = CD, ∠BAC = ∠DCA. Chứng minh rằng ΔABC = ΔCDA.
(Hình vẽ minh họa với AB và CD cắt nhau tại một điểm, ∠BAC và ∠DCA là các góc xen giữa)
Giải:
Xét ΔABC và ΔCDA, ta có:
Vậy, ΔABC = ΔCDA (trường hợp bằng nhau cạnh - góc - cạnh).
Bài 1: Cho tam giác PQR và tam giác XYZ có PQ = XY, ∠P = ∠X, và QR = YZ. Chứng minh rằng ΔPQR = ΔXYZ.
Bài 2: Cho hình vẽ, biết AM = BN, ∠A = ∠B. Chứng minh rằng ΔAMB = ΔBNA.
(Hình vẽ minh họa với AM và BN là các đoạn thẳng)
Lý thuyết hai tam giác bằng nhau và trường hợp bằng nhau thứ nhất (cạnh - góc - cạnh) là những kiến thức cơ bản và quan trọng trong hình học. Việc nắm vững lý thuyết này sẽ giúp các em giải quyết các bài toán liên quan đến tam giác một cách dễ dàng và hiệu quả hơn. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán của mình.