Chào mừng bạn đến với bài học về Lý thuyết Góc ở vị trí đặc biệt và Tia phân giác của một góc, một phần quan trọng trong chương trình Toán 7 - Kết nối tri thức.
Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản về các loại góc đặc biệt, mối quan hệ giữa chúng, và cách xác định tia phân giác của một góc.
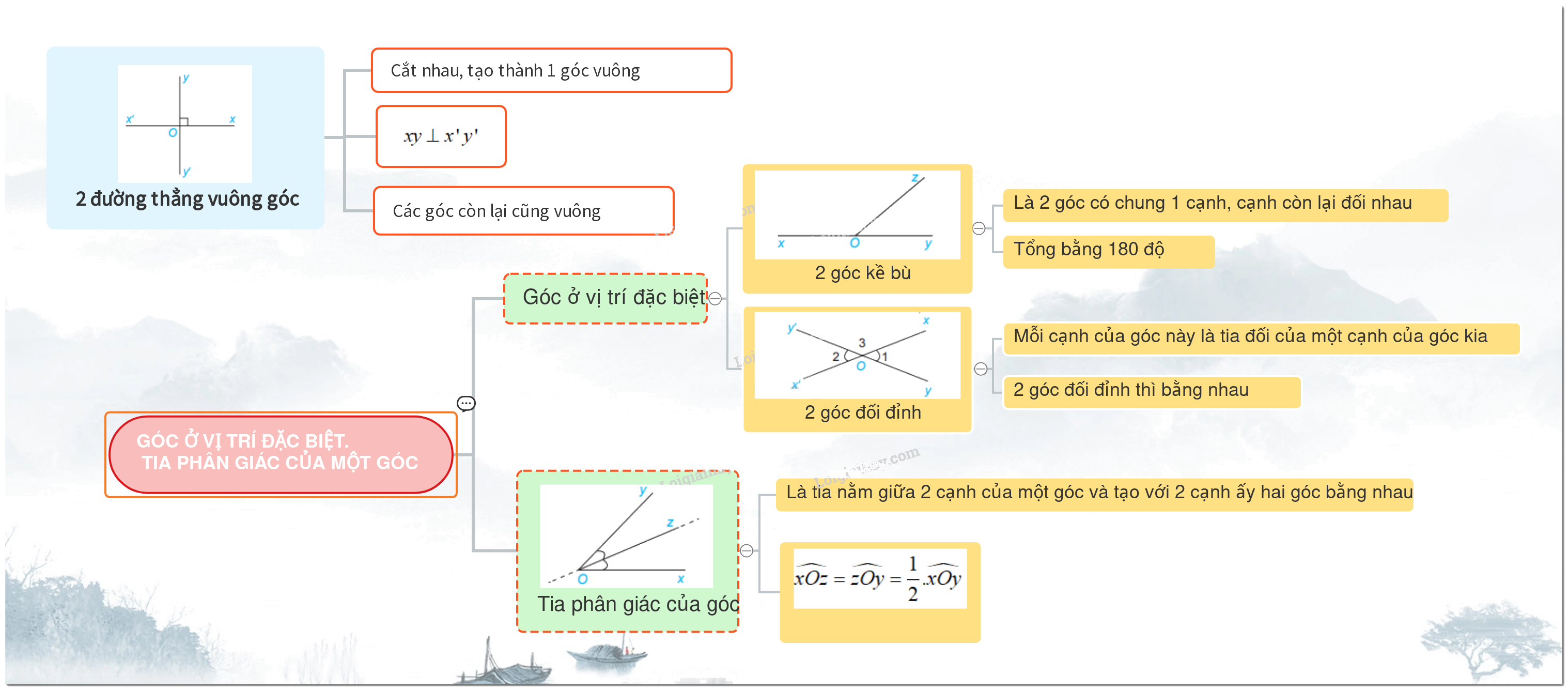
1. Góc ở vị trí đặc biệt
1. Góc ở vị trí đặc biệt
a) 2 góc kề bù
Hai góc có một cạnh chung, 2 cạnh còn lại là hai tia đối nhau được gọi là 2 góc kề bù.
* Tính chất: 2 góc kề bù có tổng số đo là 180 độ.
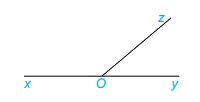
Góc xOz và góc yOz là 2 góc kề bù vì có tia Oz chung; tia Ox và Oy là 2 tia đối nhau.
Ta có: \(\widehat {xOz} + \widehat {yOz} = 180^\circ \)
Chú ý:
Nếu điểm M nằm trong góc xOy thì ta nói tia OM nằm giữa 2 tia Ox và Oy. Khi đó:
\(\widehat {xOM} + \widehat {MOy} = \widehat {xOy}\)
b) 2 góc đối đỉnh
2 góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.
* Tính chất: Hai góc đối đỉnh thì bằng nhau
Chú ý: 2 đường thẳng cắt nhau tạo thành 2 cặp góc đối đỉnh
Ví dụ:
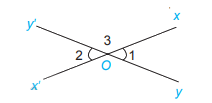
\(\widehat {{O_1}} = \widehat {{O_2}};\widehat {{O_3}} = \widehat {{O_4}}\)( đối đỉnh)
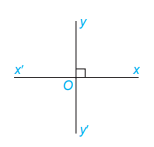
Chú ý: 2 đường thẳng cắt nhau và trong các góc tạo thành có một góc vuông thì 2 đường thẳng đó vuông góc.
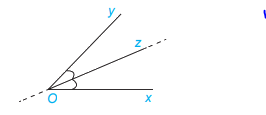
2. Tia phân giác của một góc
Định nghĩa: Tia nằm giữa 2 cạnh của một góc và tạo với 2 cạnh ấy hai góc bằng nhau được gọi là tia phân giác của góc đó.
* Tính chất: Khi Oz là tia phân giác của góc xOy thì \(\widehat {xOz} = \widehat {zOy} = \frac{1}{2}.\widehat {xOy}\)
Chú ý: Đường thẳng chứa tia phân giác của một góc là đường phân giác của góc đó.
Trong chương trình Toán 7, việc nắm vững kiến thức về góc và các vị trí đặc biệt của góc là vô cùng quan trọng. Bài viết này sẽ trình bày chi tiết lý thuyết về góc ở vị trí đặc biệt và tia phân giác của một góc, theo chương trình sách Kết nối tri thức.
Góc là hình tạo bởi hai tia chung gốc. Dựa vào số đo, góc được chia thành các loại sau:
Góc kề nhau: Hai góc có chung cạnh, chung đỉnh và không có điểm trong chung.
Góc kề bù: Hai góc kề nhau có tổng số đo bằng 180°.
Ví dụ: Nếu ∠AOB = 60° và ∠BOC = 120°, hai góc này kề nhau và ∠AOC = ∠AOB + ∠BOC = 180°, do đó ∠AOB và ∠BOC là hai góc kề bù.
Hai đường thẳng gọi là vuông góc với nhau nếu chúng cắt nhau và tạo thành một góc vuông.
Ký hiệu: a ⊥ b
Tia phân giác của một góc là tia nằm giữa hai cạnh của góc và tạo với hai cạnh đó hai góc bằng nhau.
Ví dụ: Nếu ∠AOB = 80°, tia OT là tia phân giác của ∠AOB thì ∠AOT = ∠BOT = 40°.
Bài 1: Cho ∠ABC = 70°. Vẽ tia phân giác BD của ∠ABC. Tính số đo ∠ABD.
Giải: Vì BD là tia phân giác của ∠ABC nên ∠ABD = ∠DBC = ∠ABC / 2 = 70° / 2 = 35°.
Bài 2: Hai góc kề bù có một góc bằng 45°. Tính số đo góc còn lại.
Giải: Gọi hai góc kề bù là ∠A và ∠B. Ta có ∠A + ∠B = 180°. Nếu ∠A = 45° thì ∠B = 180° - 45° = 135°.
Việc hiểu rõ lý thuyết về góc ở vị trí đặc biệt và tia phân giác của một góc là bước đầu tiên quan trọng để giải quyết các bài toán hình học trong chương trình Toán 7. Hãy luyện tập thường xuyên để nắm vững kiến thức và áp dụng thành thạo vào giải bài tập.