Bài học này sẽ cung cấp cho bạn kiến thức nền tảng về hai trường hợp bằng nhau quan trọng của tam giác trong chương trình Toán 7 - Kết nối tri thức. Chúng ta sẽ cùng nhau tìm hiểu điều kiện để hai tam giác bằng nhau theo từng trường hợp, cùng với các ví dụ minh họa cụ thể.
Nắm vững lý thuyết này là bước đệm quan trọng để giải quyết các bài tập liên quan đến tam giác bằng nhau, đồng thời phát triển tư duy logic và khả năng chứng minh hình học.
Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh (c.g.c)
1. Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh (c.g.c)
Nếu 2 cạnh và góc xen giữa của tam giác này bằng 2 cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
Ví dụ:
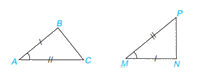
Xét 2 tam giác ABC và MNP có:
AB=MN
\(\widehat {BAC} = \widehat {NMP}\)
AC=MP
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)
2. Trường hợp bằng nhau thứ ba của tam giác: góc- cạnh - góc (g.c.g)
Nếu 1 cạnh và 2 góc kề của tam giác này bằng 1 cạnh và 2 góc kề của tam giác kia thì hai tam giác đó bằng nhau.
Ví dụ:
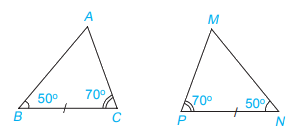
Xét 2 tam giác ABC và MNP có:
\(\begin{array}{l}\widehat B = \widehat N\\BC = NP\\\widehat C = \widehat P\end{array}\)
Vậy \(\Delta ABC = \Delta MNP\)(g.c.g)
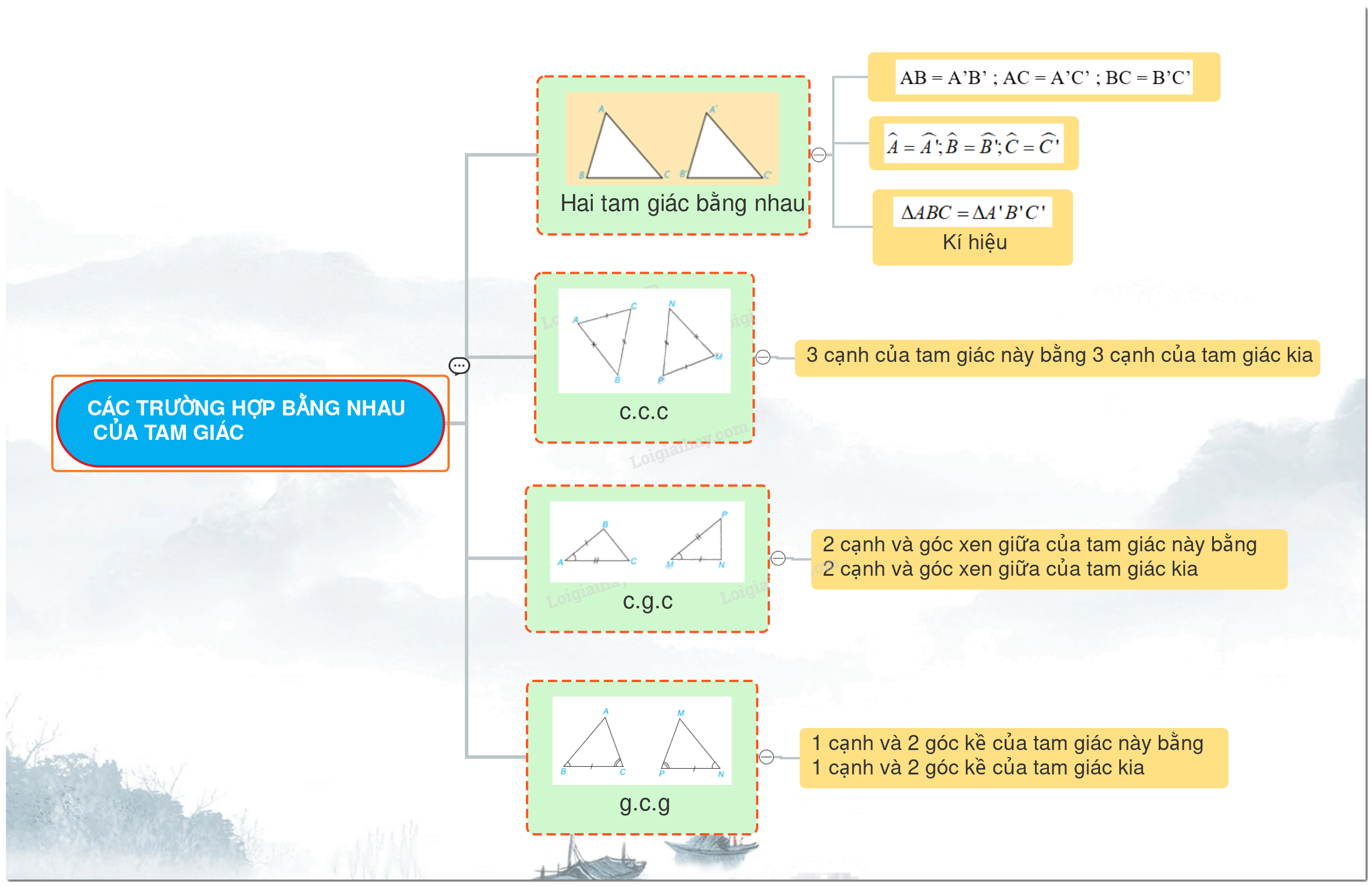
Trong chương trình Toán 7 - Kết nối tri thức, việc hiểu rõ các trường hợp bằng nhau của tam giác là vô cùng quan trọng. Bài viết này sẽ đi sâu vào lý thuyết về trường hợp bằng nhau thứ hai (cạnh - góc - cạnh) và trường hợp bằng nhau thứ ba (góc - cạnh - góc) của tam giác, cung cấp kiến thức chi tiết, dễ hiểu và bài tập vận dụng để bạn có thể nắm vững kiến thức này.
Trước khi đi vào các trường hợp bằng nhau cụ thể, chúng ta cần ôn lại khái niệm về tam giác bằng nhau. Hai tam giác được gọi là bằng nhau nếu tất cả các cạnh và các góc tương ứng của chúng bằng nhau. Điều này có nghĩa là:
Phát biểu: Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
Ký hiệu: ΔABC = ΔA'B'C' khi và chỉ khi:
Ví dụ: Cho ΔABC và ΔMNP có AB = MN, ∠A = ∠M, AC = MP. Chứng minh ΔABC = ΔMNP.
Chứng minh:
Xét ΔABC và ΔMNP, ta có:
Vậy, ΔABC = ΔMNP (trường hợp bằng nhau cạnh - góc - cạnh).
Phát biểu: Nếu hai góc và cạnh xen giữa của tam giác này bằng hai góc và cạnh xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
Ký hiệu: ΔABC = ΔA'B'C' khi và chỉ khi:
Ví dụ: Cho ΔPQR và ΔXYZ có ∠P = ∠X, PQ = XY, ∠Q = ∠Y. Chứng minh ΔPQR = ΔXYZ.
Chứng minh:
Xét ΔPQR và ΔXYZ, ta có:
Vậy, ΔPQR = ΔXYZ (trường hợp bằng nhau góc - cạnh - góc).
Bài 1: Cho ΔABC và ΔABD có AB chung, ∠BAC = ∠BAD, AC = AD. Chứng minh ΔABC = ΔABD.
Bài 2: Cho ΔMNP và ΔQRP có MN = QR, ∠M = ∠Q, NP = RP. Chứng minh ΔMNP = ΔQRP.
Bài 3: (Bài tập nâng cao) Cho tam giác ABC vuông tại A. Vẽ đường cao AH. Chứng minh ΔAHB = ΔAHC.
Khi áp dụng các trường hợp bằng nhau của tam giác, cần chú ý đến vị trí tương ứng của các cạnh và góc. Đảm bảo rằng các cạnh và góc được so sánh phải là các cạnh và góc tương ứng của hai tam giác.
Việc nắm vững các trường hợp bằng nhau của tam giác không chỉ giúp bạn giải quyết các bài tập trong sách giáo khoa mà còn là nền tảng để học các kiến thức hình học nâng cao hơn trong tương lai.
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về lý thuyết Trường hợp bằng nhau thứ hai và thứ ba của tam giác SGK Toán 7 - Kết nối tri thức. Hãy luyện tập thường xuyên để nắm vững kiến thức và áp dụng thành thạo vào giải bài tập.