Chào mừng các em học sinh đến với lời giải chi tiết mục 1 trang 33, 34 sách giáo khoa Toán 7 tập 1 chương trình Kết nối tri thức. Bài viết này sẽ cung cấp đáp án đầy đủ, chính xác và dễ hiểu cho từng bài tập, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Hãy cùng chúng tôi khám phá lời giải chi tiết ngay sau đây!
a) Trong các cách viết: ....Điểm nào trong Hình 2.4 biểu diễn số...Cho biết nếu một tam giác vuông có hai cạnh góc vuông bằng 1 và 3 thì cạnh huyền của tam giác bằng
a) Trong các cách viết: \(\sqrt 2 \in \mathbb{Q}; \pi \in \mathbb{I}; 15 \in \mathbb{R}\), cách viết nào đúng?
b) Viết số đối của các số: \(5,08(299); - \sqrt 5 \)
Phương pháp giải:
Số hữu tỉ là số viết được dưới dạng \(\frac{a}{b}(a,b \in \mathbb{Z};b \ne 0)\)
Số hữu tỉ và số vô tỉ được gọi chung là số thực
Số đối của số thực a là -a
Lời giải chi tiết:
a) Ta có: \(\sqrt 2 \notin \mathbb{Q};\pi \in \mathbb{I};15 \in \mathbb{R}\)
Vậy cách viết \(\pi \in \mathbb{I}; 15 \in \mathbb{R}\) là đúng
b) Số đối của 5,08(299) là -5,08(299)
Số đối của -\(\sqrt 5 \) là \(\sqrt 5 \)
Cho biết nếu một tam giác vuông có hai cạnh góc vuông bằng 1 và 3 thì cạnh huyền của tam giác bằng \(\sqrt {10} \). Em hãy vẽ điểm biểu diễn số - \(\sqrt {10} \) trên trục số.
Phương pháp giải:
Bước 1: Vẽ tam giác vuông có hai cạnh góc vuông bằng 1 và 3. Đo độ dài của cạnh huyền
Bước 2: Vẽ trục số. Biểu diễn số - \(\sqrt {10} \) trên trục số nằm ở bên trái gốc O, cách O một khoảng bằng độ dài cạnh huyền của tam giác vuông vừa vẽ.
Lời giải chi tiết:
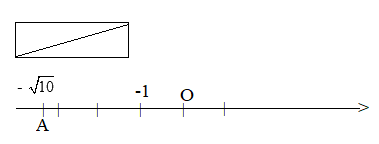
Chú ý: Các số thực âm được biểu diễn bởi các điểm nằm bên trái điểm O trên trục số.
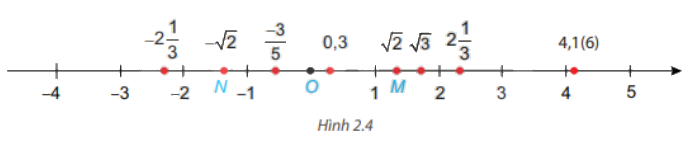
Điểm nào trong Hình 2.4 biểu diễn số \( - \sqrt 2 \)? Em có nhận xét gì về điểm biểu diễn của hai số đối nhau?
Phương pháp giải:
Quan sát trục số, tìm điểm \( - \sqrt 2 \)
Nhận xét điểm biểu diễn của hai số đối nhau
Lời giải chi tiết:
Điểm biểu diễn số \( - \sqrt 2 \) là điểm N.
Điểm biểu diễn của hai số đối nhau là 2 điểm cách đều gốc O và nằm về 2 phía của điểm O
a) Trong các cách viết: \(\sqrt 2 \in \mathbb{Q}; \pi \in \mathbb{I}; 15 \in \mathbb{R}\), cách viết nào đúng?
b) Viết số đối của các số: \(5,08(299); - \sqrt 5 \)
Phương pháp giải:
Số hữu tỉ là số viết được dưới dạng \(\frac{a}{b}(a,b \in \mathbb{Z};b \ne 0)\)
Số hữu tỉ và số vô tỉ được gọi chung là số thực
Số đối của số thực a là -a
Lời giải chi tiết:
a) Ta có: \(\sqrt 2 \notin \mathbb{Q};\pi \in \mathbb{I};15 \in \mathbb{R}\)
Vậy cách viết \(\pi \in \mathbb{I}; 15 \in \mathbb{R}\) là đúng
b) Số đối của 5,08(299) là -5,08(299)
Số đối của -\(\sqrt 5 \) là \(\sqrt 5 \)
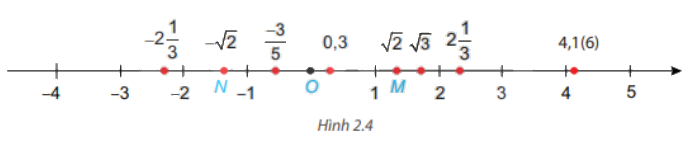
Điểm nào trong Hình 2.4 biểu diễn số \( - \sqrt 2 \)? Em có nhận xét gì về điểm biểu diễn của hai số đối nhau?
Phương pháp giải:
Quan sát trục số, tìm điểm \( - \sqrt 2 \)
Nhận xét điểm biểu diễn của hai số đối nhau
Lời giải chi tiết:
Điểm biểu diễn số \( - \sqrt 2 \) là điểm N.
Điểm biểu diễn của hai số đối nhau là 2 điểm cách đều gốc O và nằm về 2 phía của điểm O
Cho biết nếu một tam giác vuông có hai cạnh góc vuông bằng 1 và 3 thì cạnh huyền của tam giác bằng \(\sqrt {10} \). Em hãy vẽ điểm biểu diễn số - \(\sqrt {10} \) trên trục số.
Phương pháp giải:
Bước 1: Vẽ tam giác vuông có hai cạnh góc vuông bằng 1 và 3. Đo độ dài của cạnh huyền
Bước 2: Vẽ trục số. Biểu diễn số - \(\sqrt {10} \) trên trục số nằm ở bên trái gốc O, cách O một khoảng bằng độ dài cạnh huyền của tam giác vuông vừa vẽ.
Lời giải chi tiết:
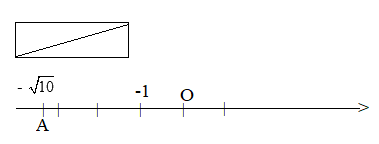
Chú ý: Các số thực âm được biểu diễn bởi các điểm nằm bên trái điểm O trên trục số.
Mục 1 trang 33, 34 SGK Toán 7 tập 1 - Kết nối tri thức tập trung vào việc ôn tập và củng cố kiến thức về các phép tính với số nguyên, số hữu tỉ, và các tính chất cơ bản của chúng. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện kỹ năng tính toán và tư duy logic.
Bài tập này yêu cầu học sinh thực hiện các phép tính cộng, trừ, nhân, chia số nguyên và số hữu tỉ. Để giải bài tập này, học sinh cần nắm vững thứ tự thực hiện các phép tính và các quy tắc dấu trong phép tính.
Bài tập này yêu cầu học sinh giải các phương trình đơn giản với số nguyên và số hữu tỉ. Để giải bài tập này, học sinh cần nắm vững các quy tắc chuyển vế và các phép biến đổi tương đương.
Bài tập này thường đưa ra một tình huống thực tế và yêu cầu học sinh vận dụng kiến thức đã học để giải quyết. Để giải bài tập này, học sinh cần đọc kỹ đề bài, xác định các yếu tố quan trọng và lập kế hoạch giải quyết.
Ví dụ: Một cửa hàng bán được 25 kg gạo trong ngày đầu tiên và 30 kg gạo trong ngày thứ hai. Hỏi trung bình mỗi ngày cửa hàng bán được bao nhiêu kg gạo?
Giải: Tổng số gạo bán được trong hai ngày là: 25 + 30 = 55 kg. Trung bình mỗi ngày cửa hàng bán được: 55 / 2 = 27.5 kg.
Ngoài sách giáo khoa, học sinh có thể tham khảo thêm các tài liệu sau để học tập và ôn luyện:
Hy vọng rằng với lời giải chi tiết và những lưu ý trên, các em học sinh sẽ tự tin hơn trong việc giải các bài tập mục 1 trang 33, 34 SGK Toán 7 tập 1 - Kết nối tri thức. Chúc các em học tập tốt!