Bài 3.8 trang 49 SGK Toán 7 tập 1 thuộc chương 3: Các góc và đường thẳng song song của sách Kết nối tri thức. Bài tập này yêu cầu học sinh vận dụng kiến thức về các góc so le trong, đồng vị, trong cùng phía để chứng minh tính chất của các đường thẳng song song.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3.8 trang 49 SGK Toán 7 tập 1, giúp các em học sinh hiểu rõ bản chất bài toán và rèn luyện kỹ năng giải toán.
Quan sát hình 3.26, giải thích vì sao AB // DC.
Đề bài
Quan sát hình 3.26, giải thích vì sao AB // DC.
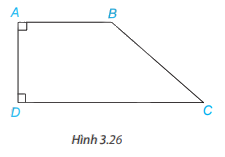
Phương pháp giải - Xem chi tiết
Nhận xét: 2 đường thẳng cùng vuông góc với đường thẳng thứ 3 thì song song với nhau
Lời giải chi tiết
Vì AB và DC cùng vuông góc với đường thẳng AD nên AB // DC ( Theo nhận xét trang 48)
Bài 3.8 trang 49 SGK Toán 7 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về các góc và đường thẳng song song. Để giải bài tập này một cách hiệu quả, các em cần nắm vững các khái niệm và tính chất sau:
Nội dung bài tập 3.8 trang 49 SGK Toán 7 tập 1 - Kết nối tri thức:
Cho hình vẽ sau (hình vẽ cần được mô tả chi tiết, ví dụ: a // b, c cắt a và b tại A và B, góc DAB = 50 độ). Chứng minh rằng a // b.
Lời giải:
Để chứng minh a // b, ta cần chứng minh một trong các điều kiện sau:
Trong trường hợp này, ta có thể chứng minh góc DAB = góc ABC (với góc ABC là góc so le trong của góc DAB). Nếu góc DAB = góc ABC, thì a // b (theo tính chất hai đường thẳng song song).
Ví dụ minh họa:
Giả sử góc DAB = 50 độ. Để chứng minh a // b, ta cần chứng minh góc ABC = 50 độ. Nếu góc ABC = 50 độ, thì a // b.
Phương pháp giải bài tập tương tự:
Khi gặp các bài tập chứng minh hai đường thẳng song song, các em cần:
Luyện tập thêm:
Các em có thể luyện tập thêm các bài tập tương tự trong SGK Toán 7 tập 1 - Kết nối tri thức và các đề thi thử để nắm vững kiến thức và kỹ năng giải bài tập.
Tổng kết:
Bài 3.8 trang 49 SGK Toán 7 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về các góc và đường thẳng song song. Hy vọng với lời giải chi tiết và phương pháp giải được trình bày ở trên, các em học sinh sẽ hiểu rõ bài toán và giải quyết nó một cách hiệu quả.