Bài 4.10 trang 69 SGK Toán 7 tập 1 thuộc chương 1: Các số hữu tỉ. Bài tập này yêu cầu học sinh vận dụng kiến thức về so sánh hai số hữu tỉ để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.10 trang 69 SGK Toán 7 tập 1 - Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Cho tam giác ABC có BCA} = 60 và điểm M nằm trên cạnh BC sao cho
Đề bài
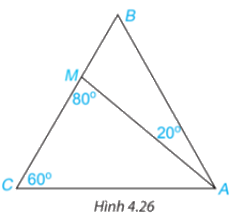
Cho tam giác ABC có \(\widehat {BCA} = {60^o}\) và điểm M nằm trên cạnh BC sao cho \(\widehat {BAM} = {20^\circ },\widehat {AMC} = {80^\circ }({\rm{H}}.4.26).\) Tính số đo các góc AMB, ABC, BAC.
Phương pháp giải - Xem chi tiết
Áp dụng:
+ Tổng ba góc trong 1 tam giác bằng 180 độ
+ Tổng hai góc kề bù bằng 180 độ.
Lời giải chi tiết
Ta có:
\(\widehat {AMB} + \widehat {AMC} = {180^o}\)( 2 góc kề bù)
\(\begin{array}{l} \Rightarrow \widehat {AMB} + {80^o} = {180^o}\\ \Rightarrow \widehat {AMB} = {100^o}\end{array}\)
Áp dụng định lí tổng ba góc trong một tam giác:
+) Trong tam giác AMB có:
\(\begin{array}{l}\widehat {ABC} + \widehat {MAB} + \widehat {AMB} = {180^O}\\ \Rightarrow \widehat {ABC} + {20^o} + {100^o} = {180^O}\\ \Rightarrow \widehat {ABC} = {60^o}\end{array}\)
+) Trong tam giác ABC có: \(\begin{array}{l}\widehat {BAC} + \widehat {ACB} + \widehat {CBA} = {180^o}\\ \Rightarrow \widehat {BAC} + {60^o} + {60^o} = {180^o}\\ \Rightarrow \widehat {BAC} = {60^o}\end{array}\)
Bài 4.10 trang 69 SGK Toán 7 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về so sánh các số hữu tỉ. Để giải bài tập này, học sinh cần nắm vững các quy tắc so sánh số hữu tỉ, bao gồm:
Bài tập yêu cầu so sánh các cặp số hữu tỉ sau:
a) So sánh -1/2 và 1/3
Để so sánh hai số hữu tỉ này, ta quy đồng mẫu số:
-1/2 = -3/6 và 1/3 = 2/6
Vì -3 < 2 nên -3/6 < 2/6, hay -1/2 < 1/3
b) So sánh -1/3 và -1/4
Để so sánh hai số hữu tỉ này, ta quy đồng mẫu số:
-1/3 = -4/12 và -1/4 = -3/12
Vì -4 < -3 nên -4/12 < -3/12, hay -1/3 < -1/4
c) So sánh 2/3 và 3/4
Để so sánh hai số hữu tỉ này, ta quy đồng mẫu số:
2/3 = 8/12 và 3/4 = 9/12
Vì 8 < 9 nên 8/12 < 9/12, hay 2/3 < 3/4
d) So sánh -2 và -1
Vì -2 < -1 nên -2 < -1
Để luyện tập thêm, các em có thể giải các bài tập tương tự sau:
Bài 4.10 trang 69 SGK Toán 7 tập 1 - Kết nối tri thức là một bài tập cơ bản về so sánh số hữu tỉ. Việc nắm vững các quy tắc so sánh và luyện tập thường xuyên sẽ giúp các em học sinh giải quyết các bài tập tương tự một cách dễ dàng và hiệu quả.
Hy vọng với lời giải chi tiết này, các em học sinh sẽ hiểu rõ hơn về cách giải bài tập so sánh số hữu tỉ và tự tin hơn trong quá trình học tập môn Toán 7.