Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 7 tập 1 - Kết nối tri thức tại giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong SGK, giúp các em nắm vững kiến thức và tự tin hơn trong học tập.
Mục 2 của chương trình Toán 7 tập 1 tập trung vào các kiến thức cơ bản về số nguyên, phép toán trên số nguyên và các tính chất quan trọng. Việc hiểu rõ và vận dụng thành thạo các kiến thức này là nền tảng cho các bài học tiếp theo.
Cắt rời một góc xOy từ một tờ giấy rồi gấp sao cho hai cạnh của góc trùng nhau (H.3.9).....Cho góc xAm có số đo bằng..
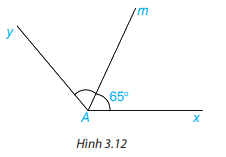
Cho góc xAm có số đo bằng \(65^\circ \) và Am là tia phân giác của góc xAy (H.3.12). Tính số đo góc xAy
Phương pháp giải:
Khi Om là tia phân giác của góc xOy thì \(\widehat {xOm} = \widehat {mOy} = \frac{1}{2}.\widehat {xOy}\)
Lời giải chi tiết:
Ta có Am là tia phân giác của góc xAy nên
\(\begin{array}{l}\widehat {xAm} = \frac{1}{2}.\widehat {xAy}\\ \Rightarrow \widehat {xAy} = 2.\widehat {xAm} = 2.65^\circ = 130^\circ \end{array}\)
Quan sát hình vẽ bên.
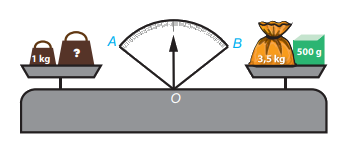
Quả cân ở đĩa cân bên trái nặng bao nhiêu kilogam để cân thăng bằng, tức là kim trên mặt đồng hồ của cân là tia phân giác của góc AOB?
Phương pháp giải:
Tổng cân nặng 2 bên cân bằng nhau thì cân thăng bằng
Lời giải chi tiết:
Đổi 500 g = 0,5 kg
Tổng cân nặng bên đĩa cân phải là: 3,5 + 0,5 = 4(kg)
Quả cân ở đĩa cân bên trái nặng số kilogam để cân thăng bằng là:
4 – 1 = 3 (kg)
Chú ý:
Cần đưa các số liệu về cùng một đơn vị đo.
Cắt rời một góc xOy từ một tờ giấy rồi gấp sao cho hai cạnh của góc trùng nhau (H.3.9).
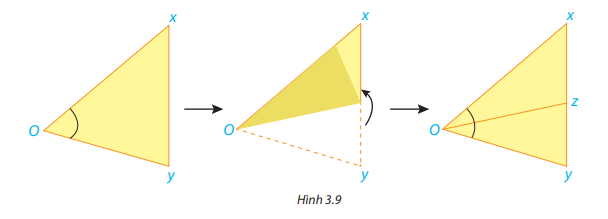
Mở mảnh giấy ra, nếp gấp cho ta hình ảnh tia Oz chia góc ban đầu thành hai góc.
a) Em hãy nhận xét về vị trí của tia Oz so với hai cạnh của góc xOy.
b) Em hãy so sánh hai góc xOz và zOy.
Phương pháp giải:
Quan sát, đo góc.
Lời giải chi tiết:
a) Tia Oz nằm giữa hai cạnh của góc xOy.
b) \(\widehat {xOz} = \widehat {zOy}\)
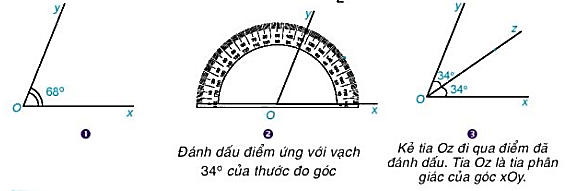
Vẽ tia phân giác Oz của xOy có số đo bằng 68\(^\circ \), sử dụng thước đo góc theo hướng dẫn. Nếu Oz là toa phân giác của góc xOy thì \(\widehat {xOz} = \frac{1}{2}.68^\circ = 34^\circ \). Ta có cách vẽ sau:
Phương pháp giải:
Tia phân giác Oz của góc xOy chia góc xOy thành 2 góc bằng nhau (bằng \(\dfrac{1}{2}\) góc xOy)
Lời giải chi tiết:
Bước 1. Vẽ góc xOy có số đo bằng \(68^0\)
Bước 2. Sử dụng thước đo độ, đánh dấu điểm ứng với vạch \(34^0\) của thước đo góc.
Bước 3. Kẻ tia Oz đi qua điểm đã đánh dấu. Tia Oz là tia phân giác của góc xOy.
Cắt rời một góc xOy từ một tờ giấy rồi gấp sao cho hai cạnh của góc trùng nhau (H.3.9).
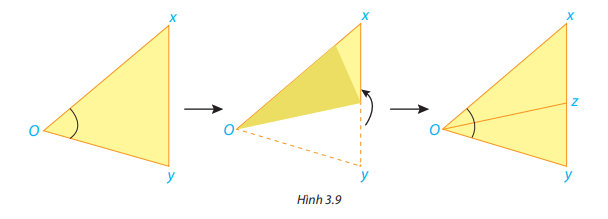
Mở mảnh giấy ra, nếp gấp cho ta hình ảnh tia Oz chia góc ban đầu thành hai góc.
a) Em hãy nhận xét về vị trí của tia Oz so với hai cạnh của góc xOy.
b) Em hãy so sánh hai góc xOz và zOy.
Phương pháp giải:
Quan sát, đo góc.
Lời giải chi tiết:
a) Tia Oz nằm giữa hai cạnh của góc xOy.
b) \(\widehat {xOz} = \widehat {zOy}\)
Cho góc xAm có số đo bằng \(65^\circ \) và Am là tia phân giác của góc xAy (H.3.12). Tính số đo góc xAy
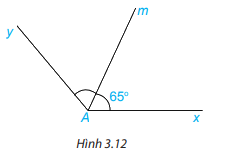
Phương pháp giải:
Khi Om là tia phân giác của góc xOy thì \(\widehat {xOm} = \widehat {mOy} = \frac{1}{2}.\widehat {xOy}\)
Lời giải chi tiết:
Ta có Am là tia phân giác của góc xAy nên
\(\begin{array}{l}\widehat {xAm} = \frac{1}{2}.\widehat {xAy}\\ \Rightarrow \widehat {xAy} = 2.\widehat {xAm} = 2.65^\circ = 130^\circ \end{array}\)
Vẽ tia phân giác Oz của xOy có số đo bằng 68\(^\circ \), sử dụng thước đo góc theo hướng dẫn. Nếu Oz là toa phân giác của góc xOy thì \(\widehat {xOz} = \frac{1}{2}.68^\circ = 34^\circ \). Ta có cách vẽ sau:
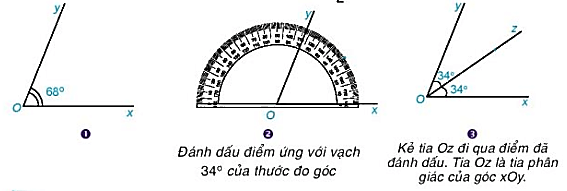
Phương pháp giải:
Tia phân giác Oz của góc xOy chia góc xOy thành 2 góc bằng nhau (bằng \(\dfrac{1}{2}\) góc xOy)
Lời giải chi tiết:
Bước 1. Vẽ góc xOy có số đo bằng \(68^0\)
Bước 2. Sử dụng thước đo độ, đánh dấu điểm ứng với vạch \(34^0\) của thước đo góc.
Bước 3. Kẻ tia Oz đi qua điểm đã đánh dấu. Tia Oz là tia phân giác của góc xOy.
Quan sát hình vẽ bên.
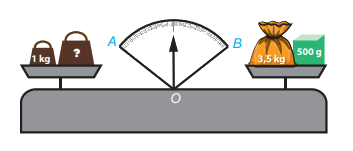
Quả cân ở đĩa cân bên trái nặng bao nhiêu kilogam để cân thăng bằng, tức là kim trên mặt đồng hồ của cân là tia phân giác của góc AOB?
Phương pháp giải:
Tổng cân nặng 2 bên cân bằng nhau thì cân thăng bằng
Lời giải chi tiết:
Đổi 500 g = 0,5 kg
Tổng cân nặng bên đĩa cân phải là: 3,5 + 0,5 = 4(kg)
Quả cân ở đĩa cân bên trái nặng số kilogam để cân thăng bằng là:
4 – 1 = 3 (kg)
Chú ý:
Cần đưa các số liệu về cùng một đơn vị đo.
Mục 2 trong SGK Toán 7 tập 1 - Kết nối tri thức bao gồm các bài tập rèn luyện về các phép toán trên số nguyên, bao gồm cộng, trừ, nhân, chia và các tính chất giao hoán, kết hợp, phân phối. Việc giải các bài tập này đòi hỏi học sinh phải nắm vững các quy tắc và tính chất cơ bản của số nguyên.
Để giải bài tập này, học sinh cần áp dụng các quy tắc về thứ tự thực hiện các phép toán (nhân, chia trước; cộng, trừ sau) và các tính chất giao hoán, kết hợp, phân phối để đơn giản hóa biểu thức. Ví dụ:
a) 12 + (-5) = 7
b) (-8) - 3 = -11
Để tìm x, học sinh cần thực hiện các phép toán ngược lại với các phép toán đã cho. Ví dụ:
a) x + 7 = 10 => x = 10 - 7 = 3
b) x - 4 = -2 => x = -2 + 4 = 2
Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để điền các số hoặc biểu thức thích hợp vào chỗ trống. Ví dụ:
a) 5 + ... = 0 => ... = -5
b) ... - 2 = -1 => ... = 1
Ngoài các dạng bài tập cơ bản như trên, còn có một số dạng bài tập khác thường gặp trong mục 2, bao gồm:
Để giải bài tập Toán 7 tập 1 - Kết nối tri thức một cách hiệu quả, học sinh cần:
| Phép toán | Quy tắc/Tính chất |
|---|---|
| Cộng | a + b = b + a (Giao hoán) |
| a + (b + c) = (a + b) + c (Kết hợp) | |
| a + 0 = a (Phần tử trung hòa) | |
| Trừ | a - b = a + (-b) |
| Nhân | a * b = b * a (Giao hoán) |
| a * (b * c) = (a * b) * c (Kết hợp) | |
| a * 1 = a (Phần tử trung hòa) | |
| a * 0 = 0 | |
| Chia | a : b = a / b (với b ≠ 0) |
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin hơn khi giải các bài tập trong mục 2 trang 43, 44, 45 SGK Toán 7 tập 1 - Kết nối tri thức. Chúc các em học tập tốt!