Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 7 tập 1 - Kết nối tri thức tại giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong SGK, giúp các em nắm vững kiến thức và tự tin hơn trong học tập.
Mục 2 của chương trình Toán 7 tập 1 tập trung vào các kiến thức cơ bản về số nguyên, phép toán trên số nguyên và các tính chất quan trọng. Việc hiểu rõ và vận dụng thành thạo các kiến thức này là nền tảng cho các bài học tiếp theo.
Vẽ tam giác ABC có ... Tương tự, vẽ thêm tam giác...Người ta dùng compa và thước thẳng để vẽ tia phân giác của góc xOy
Tương tự, vẽ thêm tam giác \({A^\prime }{B^\prime }{C^\prime }\) có \({A^\prime }{B^\prime } = 5\;{\rm{cm}},{A^\prime }{C^\prime } = 4\;{\rm{cm}},{B^\prime }{C^\prime } = 6\;{\rm{cm}}\).
- Dùng thước đo góc kiểm tra xem các góc tương ứng của hai tam giác A B C và \({A^\prime }{B^\prime }{C^\prime }\) có bằng nhau không.
- Hai tam giác A B C và \({A^\prime }{B^\prime }{C^\prime }\) có bằng nhau không?
Phương pháp giải:
- Đo các góc của hai tam giác và kết luận.
- Quan sát và chồng hai tam giác vừa vẽ lên nhau. Nếu chúng chồng khít lên nhau thì 2 tam giác đó bằng nhau.
Lời giải chi tiết:
Các góc tương ứng của hai tam giác A B C và \({A^\prime }{B^\prime }{C^\prime }\) có bằng nhau.
Hai tam giác A B C và \({A^\prime }{B^\prime }{C^\prime }\) có bằng nhau.
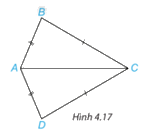
Cho hình 4.17, biết AB=AD, BC=DC. Chứng minh rằng \(\Delta ABC = \Delta ADC\)
Phương pháp giải:
Quan sát nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
Lời giải chi tiết:
Xét tam giác \(\Delta ABC\) và \(\Delta ADC\) có:
\(\begin{array}{l}AB = AD(gt)\\BC = DC(gt)\\AC\,\,\,chung\end{array}\)
Suy ra \(\Delta ABC = \Delta ADC\)(c.c.c)
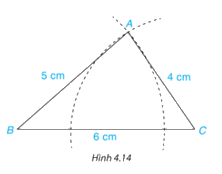
Vẽ tam giác ABC có \(AB = 5\;{\rm{cm}},AC = 4\;{\rm{cm}}\), \(BC = 6\;{\rm{cm}}\) theo các bước sau:
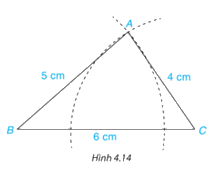
- Dùng thước thẳng có vạch chia vẽ đoạn thẳng \(BC = 6\;{\rm{cm}}\).
- Vẽ cung tròn tâm \(B\) bán kính \(5\;{\rm{cm}}\) và cung tròn tâm \(C\) bán kính \(4\;{\rm{cm}}\) sao cho hai cung tròn cắt nhau tại điểm \(A({\rm{H}}.4.14)\).
- Vẽ các đoạn thẳng A B, A C ta được tam giác ABC.
Phương pháp giải:
Vẽ hình theo các bước hướng dẫn.
Lời giải chi tiết:
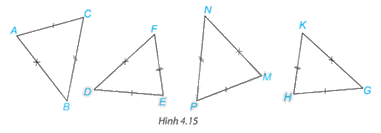
Trong Hình 4.15, những cặp tam giác nào bằng nhau?
Phương pháp giải:
Quan sát nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
Lời giải chi tiết:
Xét \(\Delta ABC\) và \(\Delta MNP\) có:
\(\begin{array}{l}AB = MN\\BC = NP\\AC = MP\end{array}\)
Vậy\(\Delta ABC\) =\(\Delta MNP\)(c.c.c)
Xét \(\Delta DEF\) và \(\Delta GHK\) có:
\(\begin{array}{l}DE = GH\\EF = HK\\DF = GK\end{array}\)
Vậy\(\Delta DEF\)=\(\Delta GHK\) (c.c.c)
Người ta dùng compa và thước thẳng để vẽ tia phân giác của góc xOy
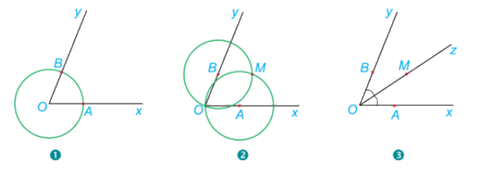
1.Vẽ đường tròn tâm O, cắt Ox và Oy lần lượt tại A và B.
2.Vẽ đường tròn tâm A bán kính AO và đường tròn tâm B bán kính BO. Hai đường tròn cắt nhau tại điểm M khác điểm O.
3. Vē tia Oz đi qua M.
Em hãy giải thích vì sao tia OM là tia phân giác của góc xOy.
Phương pháp giải:
Chứng minh hai tam giác \(\Delta OBM\) và \(\Delta OAM\) bằng nhau
Từ đó suy ra OM là tia phân giác của góc xOy.
Lời giải chi tiết:
Xét \(\Delta OBM\) và \(\Delta OAM\) có:
\(OA = OB( = R)\)
OM chung
AM=BM (do hai đường tròn tâm A và B có bán kính bằng nhau)
\( \Rightarrow \)\(\Delta OBM\) = \(\Delta OAM\)(c.c.c)
\( \Rightarrow \) \(\widehat {MOB} = \widehat {MOA}\) (hai góc tương ứng)
Mà tia OM nằm trong góc xOy
Vậy OM là tia phân giác của góc xOy.
Video hướng dẫn giải
Vẽ tam giác ABC có \(AB = 5\;{\rm{cm}},AC = 4\;{\rm{cm}}\), \(BC = 6\;{\rm{cm}}\) theo các bước sau:
- Dùng thước thẳng có vạch chia vẽ đoạn thẳng \(BC = 6\;{\rm{cm}}\).
- Vẽ cung tròn tâm \(B\) bán kính \(5\;{\rm{cm}}\) và cung tròn tâm \(C\) bán kính \(4\;{\rm{cm}}\) sao cho hai cung tròn cắt nhau tại điểm \(A({\rm{H}}.4.14)\).
- Vẽ các đoạn thẳng A B, A C ta được tam giác ABC.
Phương pháp giải:
Vẽ hình theo các bước hướng dẫn.
Lời giải chi tiết:
Tương tự, vẽ thêm tam giác \({A^\prime }{B^\prime }{C^\prime }\) có \({A^\prime }{B^\prime } = 5\;{\rm{cm}},{A^\prime }{C^\prime } = 4\;{\rm{cm}},{B^\prime }{C^\prime } = 6\;{\rm{cm}}\).
- Dùng thước đo góc kiểm tra xem các góc tương ứng của hai tam giác A B C và \({A^\prime }{B^\prime }{C^\prime }\) có bằng nhau không.
- Hai tam giác A B C và \({A^\prime }{B^\prime }{C^\prime }\) có bằng nhau không?
Phương pháp giải:
- Đo các góc của hai tam giác và kết luận.
- Quan sát và chồng hai tam giác vừa vẽ lên nhau. Nếu chúng chồng khít lên nhau thì 2 tam giác đó bằng nhau.
Lời giải chi tiết:
Các góc tương ứng của hai tam giác A B C và \({A^\prime }{B^\prime }{C^\prime }\) có bằng nhau.
Hai tam giác A B C và \({A^\prime }{B^\prime }{C^\prime }\) có bằng nhau.
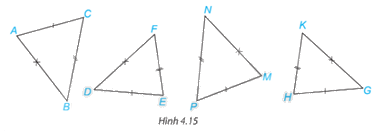
Trong Hình 4.15, những cặp tam giác nào bằng nhau?
Phương pháp giải:
Quan sát nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
Lời giải chi tiết:
Xét \(\Delta ABC\) và \(\Delta MNP\) có:
\(\begin{array}{l}AB = MN\\BC = NP\\AC = MP\end{array}\)
Vậy\(\Delta ABC\) =\(\Delta MNP\)(c.c.c)
Xét \(\Delta DEF\) và \(\Delta GHK\) có:
\(\begin{array}{l}DE = GH\\EF = HK\\DF = GK\end{array}\)
Vậy\(\Delta DEF\)=\(\Delta GHK\) (c.c.c)
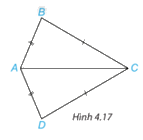
Cho hình 4.17, biết AB=AD, BC=DC. Chứng minh rằng \(\Delta ABC = \Delta ADC\)
Phương pháp giải:
Quan sát nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
Lời giải chi tiết:
Xét tam giác \(\Delta ABC\) và \(\Delta ADC\) có:
\(\begin{array}{l}AB = AD(gt)\\BC = DC(gt)\\AC\,\,\,chung\end{array}\)
Suy ra \(\Delta ABC = \Delta ADC\)(c.c.c)
Người ta dùng compa và thước thẳng để vẽ tia phân giác của góc xOy
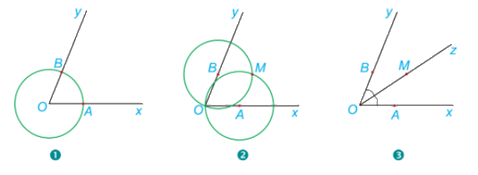
1.Vẽ đường tròn tâm O, cắt Ox và Oy lần lượt tại A và B.
2.Vẽ đường tròn tâm A bán kính AO và đường tròn tâm B bán kính BO. Hai đường tròn cắt nhau tại điểm M khác điểm O.
3. Vē tia Oz đi qua M.
Em hãy giải thích vì sao tia OM là tia phân giác của góc xOy.
Phương pháp giải:
Chứng minh hai tam giác \(\Delta OBM\) và \(\Delta OAM\) bằng nhau
Từ đó suy ra OM là tia phân giác của góc xOy.
Lời giải chi tiết:
Xét \(\Delta OBM\) và \(\Delta OAM\) có:
\(OA = OB( = R)\)
OM chung
AM=BM (do hai đường tròn tâm A và B có bán kính bằng nhau)
\( \Rightarrow \)\(\Delta OBM\) = \(\Delta OAM\)(c.c.c)
\( \Rightarrow \) \(\widehat {MOB} = \widehat {MOA}\) (hai góc tương ứng)
Mà tia OM nằm trong góc xOy
Vậy OM là tia phân giác của góc xOy.
Mục 2 trong SGK Toán 7 tập 1 - Kết nối tri thức bao gồm các bài tập rèn luyện về các phép toán cơ bản trên số nguyên, bao gồm cộng, trừ, nhân, chia. Các bài tập này không chỉ giúp học sinh củng cố kiến thức lý thuyết mà còn phát triển kỹ năng tính toán và giải quyết vấn đề.
Dưới đây là hướng dẫn giải chi tiết các bài tập trong Mục 2, trang 65, 66, 67 SGK Toán 7 tập 1 - Kết nối tri thức:
Bài tập này yêu cầu học sinh áp dụng quy tắc cộng hai số nguyên. Cần chú ý đến dấu của các số hạng để đảm bảo kết quả chính xác. Ví dụ:
a) 3 + (-5) = -2
b) (-7) + 2 = -5
Bài tập này yêu cầu học sinh áp dụng quy tắc trừ hai số nguyên. Cần đổi dấu số trừ và thực hiện phép cộng. Ví dụ:
a) 5 - (-3) = 5 + 3 = 8
b) (-4) - 2 = -4 + (-2) = -6
Bài tập này yêu cầu học sinh áp dụng quy tắc nhân hai số nguyên. Cần chú ý đến dấu của các thừa số để xác định dấu của tích. Ví dụ:
a) 2 * (-4) = -8
b) (-3) * (-5) = 15
Bài tập này yêu cầu học sinh áp dụng quy tắc chia hai số nguyên. Cần chú ý đến dấu của số chia và số bị chia để xác định dấu của thương. Ví dụ:
a) (-12) : 3 = -4
b) 10 : (-2) = -5
Bài toán: Tính giá trị của biểu thức: A = (-2) * (3 - 5) + (-4) * (-1)
Giải:
A = (-2) * (-2) + 4
A = 4 + 4
A = 8
Để củng cố kiến thức và kỹ năng giải bài tập về số nguyên, các em có thể tham khảo thêm các bài tập sau:
Việc nắm vững kiến thức và kỹ năng giải bài tập về số nguyên là rất quan trọng đối với học sinh lớp 7. Hy vọng với hướng dẫn chi tiết và các ví dụ minh họa trên, các em sẽ tự tin hơn trong việc giải các bài tập trong SGK Toán 7 tập 1 - Kết nối tri thức.