Bài 7.41 trang 45 SGK Toán 7 tập 2 thuộc chương trình Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng áp dụng các kiến thức đã học về tam giác cân vào giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 7.41 này, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Tìm số b sao cho đa thức x^3 – 3x^2 + 2x – b chia hết cho đa thức x – 3
Đề bài
Tìm số b sao cho đa thức x3 – 3x2 + 2x – b chia hết cho đa thức x – 3
Phương pháp giải - Xem chi tiết
Thực hiện phép chia đa thức cho đa thức.
Để A chia hết cho B thì số dư = 0
Lời giải chi tiết
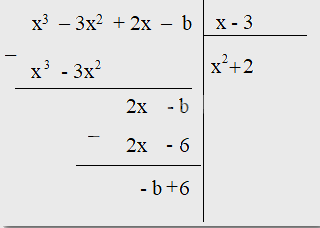
Để x3 – 3x2 + 2x – b chia hết cho đa thức x – 3 thì –b + 6 = 0 hay b = 6
Bài 7.41 yêu cầu chúng ta xét hình vẽ và chứng minh một số tính chất liên quan đến tam giác cân. Cụ thể, cho tam giác ABC cân tại A, với đường cao AH. Bài toán yêu cầu chứng minh AH là đường trung tuyến và đường phân giác của tam giác ABC.
Để giải bài toán này, chúng ta cần nắm vững các kiến thức về tam giác cân, đường cao, đường trung tuyến và đường phân giác.
Vì tam giác ABC cân tại A và AH là đường cao nên AH cũng là đường trung tuyến của tam giác ABC. Điều này có nghĩa là H là trung điểm của BC, hay BH = HC.
Giải thích: Trong một tam giác cân, đường cao xuất phát từ đỉnh góc cân đồng thời là đường trung tuyến và đường phân giác của góc ở đỉnh đó.
Vì tam giác ABC cân tại A và AH là đường cao nên AH cũng là đường phân giác của tam giác ABC. Điều này có nghĩa là góc BAH = góc CAH.
Giải thích: Tương tự như trên, trong một tam giác cân, đường cao xuất phát từ đỉnh góc cân đồng thời là đường trung tuyến và đường phân giác của góc ở đỉnh đó.
Khi giải các bài toán về tam giác cân, chúng ta cần chú ý đến các tính chất sau:
Xét tam giác ABC cân tại A, với AB = AC. Gọi M là trung điểm của BC. Chứng minh AM vuông góc với BC.
Lời giải: Xét hai tam giác ABM và ACM, ta có:
Do đó, tam giác ABM = tam giác ACM (c-c-c). Suy ra góc AMB = góc AMC. Mà góc AMB + góc AMC = 180 độ (kề bù) nên góc AMB = góc AMC = 90 độ. Vậy AM vuông góc với BC.
Cho tam giác ABC cân tại B, với đường cao BH. Chứng minh BH là đường trung tuyến và đường phân giác của tam giác ABC.
Bài 7.41 trang 45 SGK Toán 7 tập 2 - Kết nối tri thức là một bài tập cơ bản về tam giác cân. Việc nắm vững các tính chất của tam giác cân và áp dụng chúng một cách linh hoạt sẽ giúp chúng ta giải quyết bài toán một cách dễ dàng.
Để củng cố kiến thức về tam giác cân, các em học sinh nên luyện tập thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác.
| Tính chất | Mô tả |
|---|---|
| Hai cạnh bên | Bằng nhau |
| Hai góc đáy | Bằng nhau |
| Đường cao | Đồng thời là đường trung tuyến và đường phân giác của góc ở đỉnh |