Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 7 tại giaitoan.edu.vn. Chúng tôi xin giới thiệu lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 75, 76, 77 sách giáo khoa Toán 7 tập 1 - Kết nối tri thức.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi cam kết cung cấp cho các em những phương pháp giải bài tập hiệu quả nhất, giúp các em nắm vững kiến thức và tự tin hơn trong học tập.
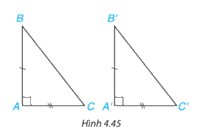
Hai tam giác vuông ABC (vuông tại đỉnh A) và A’B’C’ (vuông tại đỉnh A’) có các cặp cạnh góc vuông bằng nhau: AB = A'B', AC = A'C' (H.4.45). Dựa vào trường hợp bằng nhau cạnh - góc - cạnh của hai tam giác, hãy giải thích vì sao hai tam giác vuông ABC và ABC bằng nhau.
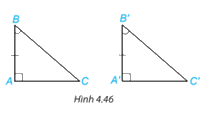
Hai tam giác vuông ABC (vuông tại đỉnh A) và ABC vuông tại đỉnh A) có tương ứng một cạnh góc vuông và một góc nhọn kề với cạnh ấy bằng nhau: AB = A'B', \(\widehat B = \widehat {B'}\) (H.4.46).
Dựa vào trường hợp bằng nhau góc cạnh - góc của hai tam giác, hãy giải thích vì sao hai tam giác vuông ABC và ABC bằng nhau.
Phương pháp giải:
Chứng minh 2 tam giác bằng nhau theo trường hợp góc - cạnh - góc.
Lời giải chi tiết:
Xét 2 tam giác ABC và A'B'C' có:
\(\widehat B = \widehat {B'}\) (gt)
AB=A’B’ (gt)
\(\widehat A = \widehat {A'}\) (gt)
\( \Rightarrow \Delta ABC = \Delta A'B'C'\)(g.c.g)
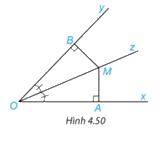
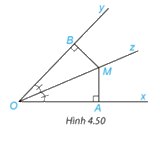
Cho Oz là tia phân giác của góc xOy. Lấy điểm M trên tia Oz và hai điểm A, B lần lượt trên các tia Ox, Oy sao cho MA vuông góc với Ox, MB vuông góc với Oy(H.4.50). Chứng minh rằng MA = MB.
Phương pháp giải:
Chứng minh hai tam giác OBM và OAM bằng nhau.
Lời giải chi tiết:
Xét hai tam giác vuông OBM và OAM có:
OM chung
\(\widehat {BOM} = \widehat {AOM}\) (gt)
\( \Rightarrow \Delta OBM = \Delta OAM\)(cạnh huyền – góc nhọn)
Suy ra MB=MA ( 2 cạnh tương ứng)
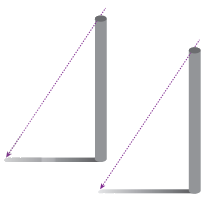
Quay lại tình huống mở đầu, ta thấy mỗi chiếc cột với bóng của nó tạo thành hai cạnh góc vuông của một tam giác vuông. Hai tam giác vuông này có hai cặp cạnh tương ứng bằng nhau và hai góc ở đỉnh chiếc cột của hai tam giác vuông này cũng bằng nhau. Vậy lí do mà bạn Tròn đưa ra có đúng không?

Phương pháp giải:
Áp dụng trường hợp bằng nhau của tam giác vuông.
Lời giải chi tiết:
Lí do mà bạn Tròn đưa ra là đúng. Vì hai tam giác vuông này bằng nhau ( g-c-g)
Hai tam giác vuông ABC (vuông tại đỉnh A) và A’B’C’ (vuông tại đỉnh A’) có các cặp cạnh góc vuông bằng nhau: AB = A'B', AC = A'C' (H.4.45). Dựa vào trường hợp bằng nhau cạnh - góc - cạnh của hai tam giác, hãy giải thích vì sao hai tam giác vuông ABC và ABC bằng nhau.
Phương pháp giải:
Chứng minh hai cạnh và góc xen giữa của hai tam giác trên bằng nhau.
Lời giải chi tiết:
Xét 2 tam giác ABC và A’B’C có:
AB=A’B’ (gt)
\(\widehat A = \widehat {A'}\) (gt)
AC=A’C’ (gt)
\( \Rightarrow \Delta ABC = \Delta A'B'C'\)(c.g.c)
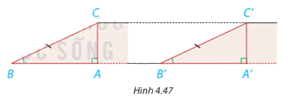
Hình 4.47 mô phỏng chiều dài và độ dốc của hai con dốcbởi các đường thẳng BC, B’C’và các góc B, B’. Khi đó AC,A’C’ mô tả độ cao của haicon dốc.
a) Dựa vào trường hợp bằng nhau góc - cạnh - góc của hai tam giác, hãy giải thích vì sao hai tam giác vuông ABC và A’B’C’ bằng nhau.
b) So sánh độ cao của hai con dốc.
Phương pháp giải:
a) Chứng minh hai tam giác bằng nhau theo trường hợp cạnh huyền – góc nhọn
b) Chứng minh AC=A’C’
Lời giải chi tiết:
a)Xét hai tam giác vuông ABC và A’B’C’ có:
BC=B’C’ (gt)
\(\widehat {ABC} = \widehat {A'B'C'}\) (gt)
\( \Rightarrow \Delta ABC = \Delta A'B'C'\)(cạnh huyền – góc nhọn)
b)Do \(\Delta ABC = \Delta A'B'C'\) nên AC=A’C’ ( 2 cạnh tương ứng)
Vậy độ cao hai con dốc bằng nhau.
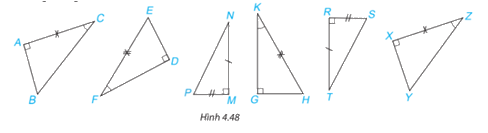
Trong Hình 4.48, hãy tìm các cặp tam giác vuông bằng nhau và giải thích vì sao chúng bằng nhau.

Phương pháp giải:
Chứng minh ba cặp tam giác vuông bằng nhau theo các trường hợp bằng nhau đã học.
Lời giải chi tiết:
+)Xét hai tam giác vuông ABC và XYZ có:
\(\widehat A = \widehat X( = 90^\circ )\) (gt)
AC=XZ (gt)
\(\widehat C = \widehat Z\) (gt)
\( \Rightarrow \Delta ABC = \Delta XYZ\) (g.c.g)
+)Xét hai tam giác vuông DEF và GHK có:
\(EF = HK\) (gt)
\(\widehat {EFD} = \widehat {GKH}\) (gt)
\( \Rightarrow \Delta DEF = \Delta GHK\) (cạnh huyền – góc nhọn)
+)Xét hai tam giác vuông MNP và RTS có:
\(MN = TR\) (gt)
\(\widehat R = \widehat M( = 90^\circ )\) (gt)
\(PM = SR\) (gt)
\( \Rightarrow \Delta MNP = \Delta RTS\) (c.g.c)
Hai tam giác vuông ABC (vuông tại đỉnh A) và A’B’C’ (vuông tại đỉnh A’) có các cặp cạnh góc vuông bằng nhau: AB = A'B', AC = A'C' (H.4.45). Dựa vào trường hợp bằng nhau cạnh - góc - cạnh của hai tam giác, hãy giải thích vì sao hai tam giác vuông ABC và ABC bằng nhau.
Phương pháp giải:
Chứng minh hai cạnh và góc xen giữa của hai tam giác trên bằng nhau.
Lời giải chi tiết:
Xét 2 tam giác ABC và A’B’C có:
AB=A’B’ (gt)
\(\widehat A = \widehat {A'}\) (gt)
AC=A’C’ (gt)
\( \Rightarrow \Delta ABC = \Delta A'B'C'\)(c.g.c)
Hai tam giác vuông ABC (vuông tại đỉnh A) và ABC vuông tại đỉnh A) có tương ứng một cạnh góc vuông và một góc nhọn kề với cạnh ấy bằng nhau: AB = A'B', \(\widehat B = \widehat {B'}\) (H.4.46).
Dựa vào trường hợp bằng nhau góc cạnh - góc của hai tam giác, hãy giải thích vì sao hai tam giác vuông ABC và ABC bằng nhau.
Phương pháp giải:
Chứng minh 2 tam giác bằng nhau theo trường hợp góc - cạnh - góc.
Lời giải chi tiết:
Xét 2 tam giác ABC và A'B'C' có:
\(\widehat B = \widehat {B'}\) (gt)
AB=A’B’ (gt)
\(\widehat A = \widehat {A'}\) (gt)
\( \Rightarrow \Delta ABC = \Delta A'B'C'\)(g.c.g)
Quay lại tình huống mở đầu, ta thấy mỗi chiếc cột với bóng của nó tạo thành hai cạnh góc vuông của một tam giác vuông. Hai tam giác vuông này có hai cặp cạnh tương ứng bằng nhau và hai góc ở đỉnh chiếc cột của hai tam giác vuông này cũng bằng nhau. Vậy lí do mà bạn Tròn đưa ra có đúng không?
Phương pháp giải:
Áp dụng trường hợp bằng nhau của tam giác vuông.
Lời giải chi tiết:
Lí do mà bạn Tròn đưa ra là đúng. Vì hai tam giác vuông này bằng nhau ( g-c-g)
Hình 4.47 mô phỏng chiều dài và độ dốc của hai con dốcbởi các đường thẳng BC, B’C’và các góc B, B’. Khi đó AC,A’C’ mô tả độ cao của haicon dốc.
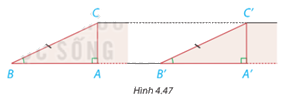
a) Dựa vào trường hợp bằng nhau góc - cạnh - góc của hai tam giác, hãy giải thích vì sao hai tam giác vuông ABC và A’B’C’ bằng nhau.
b) So sánh độ cao của hai con dốc.
Phương pháp giải:
a) Chứng minh hai tam giác bằng nhau theo trường hợp cạnh huyền – góc nhọn
b) Chứng minh AC=A’C’
Lời giải chi tiết:
a)Xét hai tam giác vuông ABC và A’B’C’ có:
BC=B’C’ (gt)
\(\widehat {ABC} = \widehat {A'B'C'}\) (gt)
\( \Rightarrow \Delta ABC = \Delta A'B'C'\)(cạnh huyền – góc nhọn)
b)Do \(\Delta ABC = \Delta A'B'C'\) nên AC=A’C’ ( 2 cạnh tương ứng)
Vậy độ cao hai con dốc bằng nhau.
Trong Hình 4.48, hãy tìm các cặp tam giác vuông bằng nhau và giải thích vì sao chúng bằng nhau.
Phương pháp giải:
Chứng minh ba cặp tam giác vuông bằng nhau theo các trường hợp bằng nhau đã học.
Lời giải chi tiết:
+)Xét hai tam giác vuông ABC và XYZ có:
\(\widehat A = \widehat X( = 90^\circ )\) (gt)
AC=XZ (gt)
\(\widehat C = \widehat Z\) (gt)
\( \Rightarrow \Delta ABC = \Delta XYZ\) (g.c.g)
+)Xét hai tam giác vuông DEF và GHK có:
\(EF = HK\) (gt)
\(\widehat {EFD} = \widehat {GKH}\) (gt)
\( \Rightarrow \Delta DEF = \Delta GHK\) (cạnh huyền – góc nhọn)
+)Xét hai tam giác vuông MNP và RTS có:
\(MN = TR\) (gt)
\(\widehat R = \widehat M( = 90^\circ )\) (gt)
\(PM = SR\) (gt)
\( \Rightarrow \Delta MNP = \Delta RTS\) (c.g.c)
Cho Oz là tia phân giác của góc xOy. Lấy điểm M trên tia Oz và hai điểm A, B lần lượt trên các tia Ox, Oy sao cho MA vuông góc với Ox, MB vuông góc với Oy(H.4.50). Chứng minh rằng MA = MB.
Phương pháp giải:
Chứng minh hai tam giác OBM và OAM bằng nhau.
Lời giải chi tiết:
Xét hai tam giác vuông OBM và OAM có:
OM chung
\(\widehat {BOM} = \widehat {AOM}\) (gt)
\( \Rightarrow \Delta OBM = \Delta OAM\)(cạnh huyền – góc nhọn)
Suy ra MB=MA ( 2 cạnh tương ứng)
Mục 1 của chương trình Toán 7 tập 1 - Kết nối tri thức tập trung vào việc ôn tập và mở rộng kiến thức về các phép toán cơ bản trên số nguyên, số hữu tỉ. Các bài tập trong trang 75, 76, 77 SGK Toán 7 tập 1 yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện kỹ năng tính toán và tư duy logic.
Bài 1 yêu cầu học sinh thực hiện các phép tính cộng, trừ, nhân, chia số nguyên và số hữu tỉ. Để giải bài tập này, học sinh cần nắm vững các quy tắc về thứ tự thực hiện các phép toán, quy tắc dấu trong phép cộng, trừ, nhân, chia.
Bài 2 yêu cầu học sinh tìm giá trị của x thỏa mãn các phương trình đơn giản. Để giải bài tập này, học sinh cần sử dụng các phép biến đổi tương đương để đưa phương trình về dạng x = a, trong đó a là một số cụ thể.
Bài 3 thường là các bài toán ứng dụng thực tế, yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các vấn đề liên quan đến cuộc sống hàng ngày. Để giải bài tập này, học sinh cần đọc kỹ đề bài, xác định các yếu tố quan trọng và xây dựng phương trình toán học phù hợp.
Ví dụ 3: Một cửa hàng bán được 25 kg gạo tẻ và 18 kg gạo nếp. Giá mỗi kg gạo tẻ là 20.000 đồng và giá mỗi kg gạo nếp là 25.000 đồng. Hỏi cửa hàng thu được bao nhiêu tiền từ việc bán gạo?
Giải:
Ngoài sách giáo khoa, học sinh có thể tham khảo thêm các tài liệu sau để nâng cao kiến thức và kỹ năng giải bài tập:
Hy vọng với lời giải chi tiết và các mẹo giải bài tập hiệu quả trên đây, các em học sinh sẽ tự tin hơn trong việc học tập môn Toán 7. Chúc các em học tốt!