Bài học về Lý thuyết Tiên đề Euclid và tính chất của hai đường thẳng song song là một phần quan trọng trong chương trình Toán 7 - Kết nối tri thức.
Nắm vững kiến thức này không chỉ giúp các em giải quyết các bài tập trong SGK mà còn là nền tảng vững chắc cho các kiến thức hình học nâng cao hơn.
Giaitoan.edu.vn cung cấp bài giảng chi tiết, dễ hiểu cùng với các bài tập có đáp án để các em có thể tự học và ôn luyện hiệu quả.
1. Tiên đề Euclid
1. Tiên đề Euclid
Qua một điểm nằm ngoài một đường thẳng, chỉ có một đường thẳng song song với đường thẳng đó.
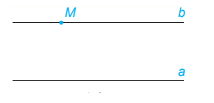
Chú ý: Nếu một đường thẳng cắt 1 trong 2 đường thẳng song song thì nó cũng cắt đường thẳng còn lại.
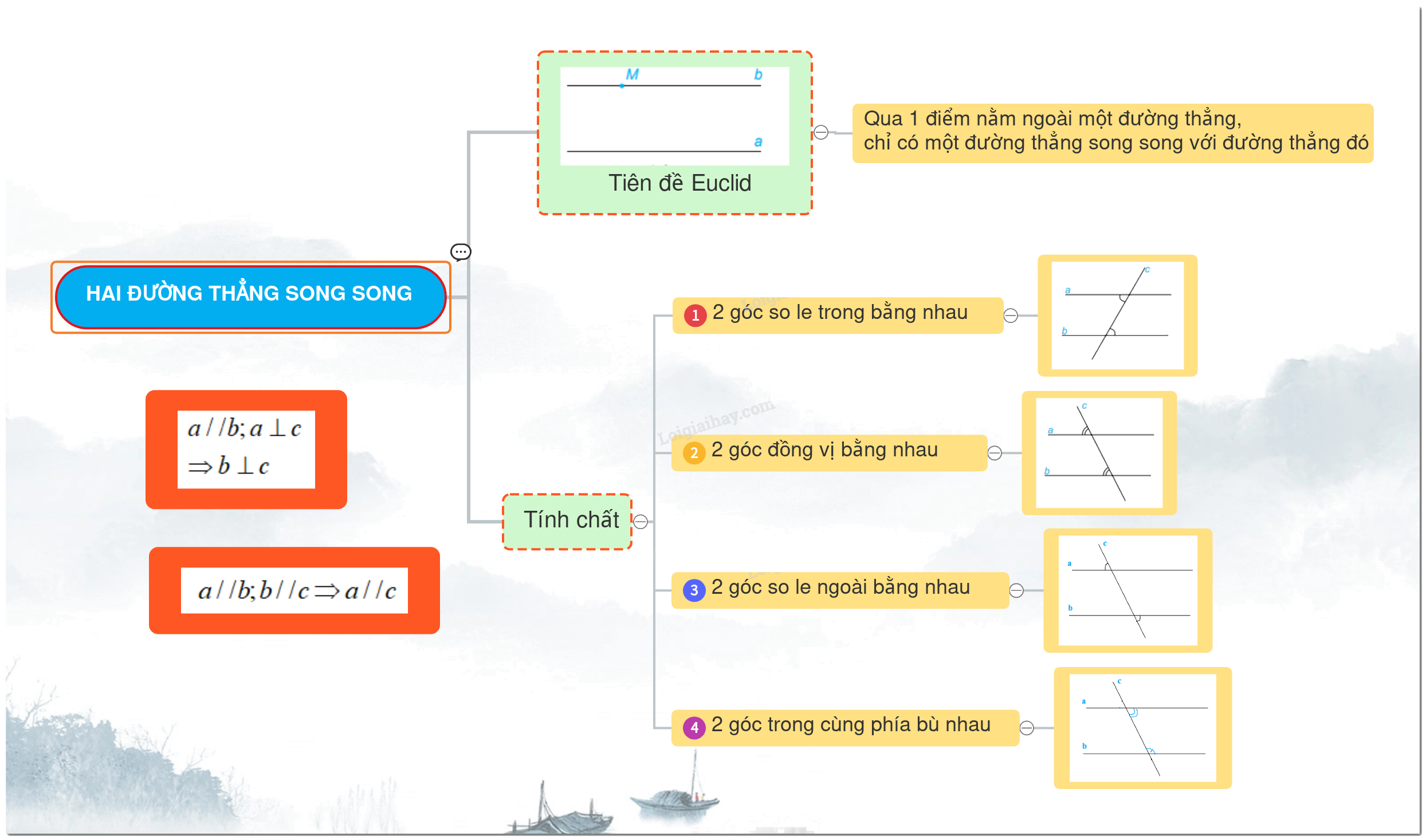
2. Tính chất của hai đường thẳng song song
Nếu một đường thẳng cắt hai đường thẳng song song thì:
+ Hai góc so le trong bằng nhau
+ Hai góc đồng vị bằng nhau
Chú ý:
+ Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng kia.
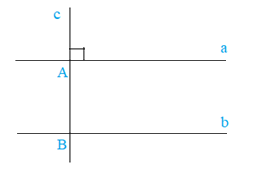
Nếu c \( \bot \) a, a // b thì c \( \bot \) b
+ Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì chúng song song với nhau.

Nếu a // b ; b // c thì a // c
Trong chương trình Toán 7, việc hiểu rõ về Tiên đề Euclid và các tính chất của đường thẳng song song là vô cùng quan trọng. Đây là nền tảng cơ bản cho việc học hình học, giúp học sinh phát triển tư duy logic và khả năng chứng minh.
Tiên đề Euclid, hay còn gọi là tiên đề thứ năm của Euclid, phát biểu rằng: “Qua một điểm nằm ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.” Tiên đề này có vai trò then chốt trong việc xây dựng hình học phẳng Euclid mà chúng ta học.
Dựa trên Tiên đề Euclid, chúng ta có thể suy ra một số tính chất quan trọng của hai đường thẳng song song:
Các tính chất trên được sử dụng rộng rãi trong việc giải các bài toán liên quan đến đường thẳng song song, góc và tam giác. Ví dụ:
Ví dụ 1: Cho hình vẽ, biết AB // CD và góc A = 60o. Tính góc C.
Giải: Vì AB // CD nên góc A và góc C là hai góc đồng vị, do đó góc C = góc A = 60o.
Để củng cố kiến thức, chúng ta cùng giải một số bài tập vận dụng:
Ngoài các tính chất cơ bản, còn có một số định lý và hệ quả liên quan đến đường thẳng song song, như định lý về đường trung bình của tam giác, định lý Thales. Việc nắm vững các kiến thức này sẽ giúp học sinh giải quyết các bài toán phức tạp hơn.
Để học tốt phần Lý thuyết Tiên đề Euclid và Tính chất của hai đường thẳng song song, các em nên:
| Tính chất | Mô tả |
|---|---|
| So le trong | Hai góc nằm bên trong hai đường thẳng song song và ở hai phía của đường thẳng cắt. |
| Đồng vị | Hai góc nằm ở cùng phía của đường thẳng cắt và có vị trí tương ứng. |
| Trong cùng phía | Hai góc nằm bên trong hai đường thẳng song song và ở cùng một phía của đường thẳng cắt. |
Hy vọng với những kiến thức và bài tập trên, các em sẽ nắm vững Lý thuyết Tiên đề Euclid và Tính chất của hai đường thẳng song song, từ đó đạt kết quả tốt trong môn Toán 7.