Giaitoan.edu.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 1 trang 31, 32 sách giáo khoa Toán 7 tập 2 chương trình Kết nối tri thức. Bài viết này sẽ giúp các em học sinh nắm vững kiến thức, hiểu rõ phương pháp giải bài tập và tự tin hơn trong quá trình học tập môn Toán.
Chúng tôi luôn cố gắng cung cấp những giải pháp học tập tốt nhất, giúp các em học Toán một cách hiệu quả và thú vị.
Tìm tổng của hai đa thức: x^3 – 5x + 2 và x^3 – x^2 +6x – 4.
Đặt tính cộng để tìm tổng của ba đa thức sau:
A = 2x3 – 5x2 + x – 7
B = x2 – 2x + 6
C = -x3 + 4x2 - 1
Phương pháp giải:
Đặt tính cộng sao cho các hạng tử cùng bậc đặt thẳng cột với nhau rồi cộng theo từng cột.
Lời giải chi tiết:
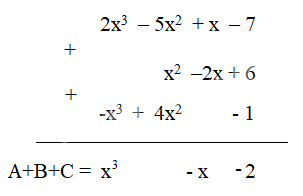
Tìm tổng của hai đa thức: x3 – 5x + 2 và x3 – x2 +6x – 4.
Phương pháp giải:
Cách 1: Bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc.
Cách 2: Đặt tính cộng sao cho các hạng tử cùng bậc đặt thẳng cột với nhau rồi cộng theo từng cột.
Lời giải chi tiết:
Cách 1:
(x3 – 5x + 2) + (x3 – x2 +6x – 4)
= x3 – 5x + 2 + x3 – x2 +6x – 4
=(x3 + x3 ) – x2 + (– 5x + 6x) + (2 – 4)
= 2x3 – x2 + x – 2
Cách 2:
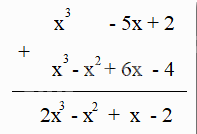
Cho hai đa thức M = 0,5x4 – 4x3 + 2x – 2,5 và N = 2x3 + x2 + 1,5
Hãy tính tổng M + N ( trình bày theo 2 cách)
Phương pháp giải:
Cách 1: Bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc.
Cách 2: Đặt tính cộng sao cho các hạng tử cùng bậc đặt thẳng cột với nhau rồi cộng theo từng cột.
Lời giải chi tiết:
Cách 1:
M + N = (0,5x4 – 4x3 + 2x – 2,5) + ( 2x3 + x2 + 1,5)
= 0,5x4 – 4x3 + 2x – 2,5 + 2x3 + x2 + 1,5
= 0,5x4 + (– 4x3 + 2x3 ) + x2 + 2x + (-2,5 + 1,5)
= 0,5x4 + (– 2x3 ) + x2 + 2x + (-1)
= 0,5x4 – 2x3 + x2 + 2x – 1
Cách 2:
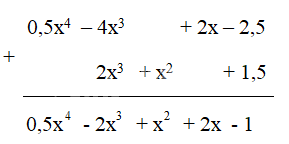
1. Cộng hai đa thức một biến
Tìm tổng của hai đa thức: x3 – 5x + 2 và x3 – x2 +6x – 4.
Phương pháp giải:
Cách 1: Bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc.
Cách 2: Đặt tính cộng sao cho các hạng tử cùng bậc đặt thẳng cột với nhau rồi cộng theo từng cột.
Lời giải chi tiết:
Cách 1:
(x3 – 5x + 2) + (x3 – x2 +6x – 4)
= x3 – 5x + 2 + x3 – x2 +6x – 4
=(x3 + x3 ) – x2 + (– 5x + 6x) + (2 – 4)
= 2x3 – x2 + x – 2
Cách 2:
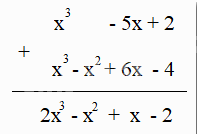
Cho hai đa thức M = 0,5x4 – 4x3 + 2x – 2,5 và N = 2x3 + x2 + 1,5
Hãy tính tổng M + N ( trình bày theo 2 cách)
Phương pháp giải:
Cách 1: Bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc.
Cách 2: Đặt tính cộng sao cho các hạng tử cùng bậc đặt thẳng cột với nhau rồi cộng theo từng cột.
Lời giải chi tiết:
Cách 1:
M + N = (0,5x4 – 4x3 + 2x – 2,5) + ( 2x3 + x2 + 1,5)
= 0,5x4 – 4x3 + 2x – 2,5 + 2x3 + x2 + 1,5
= 0,5x4 + (– 4x3 + 2x3 ) + x2 + 2x + (-2,5 + 1,5)
= 0,5x4 + (– 2x3 ) + x2 + 2x + (-1)
= 0,5x4 – 2x3 + x2 + 2x – 1
Cách 2:
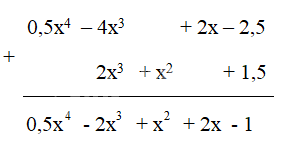
Đặt tính cộng để tìm tổng của ba đa thức sau:
A = 2x3 – 5x2 + x – 7
B = x2 – 2x + 6
C = -x3 + 4x2 - 1
Phương pháp giải:
Đặt tính cộng sao cho các hạng tử cùng bậc đặt thẳng cột với nhau rồi cộng theo từng cột.
Lời giải chi tiết:
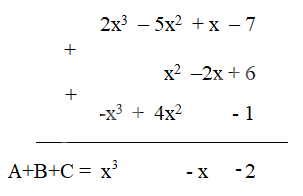
Mục 1 trang 31, 32 SGK Toán 7 tập 2 - Kết nối tri thức tập trung vào việc ôn tập và củng cố kiến thức về các phép toán với số hữu tỉ, bao gồm cộng, trừ, nhân, chia. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các quy tắc, tính chất của các phép toán để giải quyết các bài toán thực tế.
Bài tập này yêu cầu học sinh thực hiện các phép tính cộng, trừ, nhân, chia số hữu tỉ. Để giải bài tập này, học sinh cần nắm vững các quy tắc về dấu của số hữu tỉ, quy tắc cộng, trừ, nhân, chia số hữu tỉ.
Bài tập này yêu cầu học sinh giải các phương trình đơn giản với số hữu tỉ. Để giải bài tập này, học sinh cần nắm vững các quy tắc về chuyển vế, cộng, trừ, nhân, chia số hữu tỉ.
Bài tập này yêu cầu học sinh vận dụng kiến thức về các phép toán với số hữu tỉ để giải quyết các bài toán thực tế. Để giải bài tập này, học sinh cần đọc kỹ đề bài, xác định các dữ kiện và yêu cầu của bài toán, sau đó vận dụng các kiến thức đã học để giải quyết bài toán.
Ví dụ: Một người nông dân có một mảnh đất hình chữ nhật, chiều dài là 10m, chiều rộng là 5m. Người nông dân muốn trồng rau trên mảnh đất đó. Hỏi diện tích mảnh đất là bao nhiêu?
Giải: Diện tích mảnh đất là: 10m * 5m = 50m2.
Ngoài sách giáo khoa, học sinh có thể tham khảo thêm các tài liệu sau để học Toán 7:
Hy vọng rằng, với lời giải chi tiết và dễ hiểu cho mục 1 trang 31, 32 SGK Toán 7 tập 2 - Kết nối tri thức, các em học sinh sẽ học Toán 7 một cách hiệu quả và đạt kết quả tốt.