Chào mừng bạn đến với bài học về Lý thuyết Tập hợp các số hữu tỉ, một phần quan trọng trong chương trình Toán 7 - Kết nối tri thức. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản nhất về số hữu tỉ, cách nhận biết và biểu diễn chúng.
Tại giaitoan.edu.vn, chúng tôi cam kết mang đến cho bạn những bài giảng chất lượng, dễ hiểu và nhiều bài tập thực hành để bạn có thể tự tin chinh phục môn Toán.
1. Khái niệm số hữu tỉ và biểu diễn số hữu tỉ trên trục số
1. Khái niệm số hữu tỉ và biểu diễn số hữu tỉ trên trục số
Số hữu tỉ là số viết được dưới dạng phân số \(\frac{a}{b}(a,b \in \mathbb{Z};b \ne 0)\)
Tập hợp các số hữu tỉ được kí hiệu là Q
Ví dụ: \( - 7,21;\frac{{ - 7}}{{ - 9}};\frac{0}{{ - 2}};2\frac{3}{8};...\) là các số hữu tỉ
Chú ý :
+ Mỗi số hữu tỉ đều có một số đối. Số đối của số hữu tỉ \(\frac{a}{b}\) là số hữu tỉ -\(\frac{a}{b}\)
+ Các số thập phân đã biết đều là các số hữu tỉ. Các số nguyên, hỗn số cũng là các số hữu tỉ
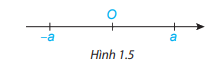
Trên trục số, điểm biểu diễn số hữu tỉ a được gọi là điểm a.
Trên trục số, 2 điểm biểu diễn 2 số hữu tỉ đối nhau a và –a nằm về 2 phía khác nhau so với điểm O và có cùng khoảng cách đến O.
2. Thứ tự trong tập hợp các số hữu tỉ
+ Ta có thể so sánh hai số hữu tỉ bất kì bằng cách viết chúng dưới dạng phân số rồi so sánh 2 phân số đó.
+ Với 2 số hữu tỉ a và b bất kì, ta luôn có hoặc a = b, hoặc a < b, hoặc a > b
+ Cho 3 số hữu tỉ a, b, c. Nếu a < b; b < c thì a < c (Tính chất bắc cầu)
+ Trên trục số, nếu a < b thì điểm a nằm trước điểm b
+ Các số hữu tỉ lớn hơn 0 gọi là các số hữu tỉ dương.
+ Các số hữu tỉ nhỏ hơn 0 gọi là các số hữu tỉ âm.
+ Số 0 không là số hữu tỉ âm, cũng không là số hữu tỉ dương.
Chú ý: Trên trục số, các điểm nằm trước gốc O biểu diễn số hữu tỉ âm; các điểm nằm sau gốc O biểu diễn số hữu tỉ dương.
Trong chương trình Toán 7, tập hợp các số hữu tỉ đóng vai trò nền tảng, giúp học sinh xây dựng kiến thức cho các chương trình học nâng cao hơn. Bài viết này sẽ trình bày chi tiết lý thuyết về tập hợp các số hữu tỉ theo sách giáo khoa Toán 7 - Kết nối tri thức, kèm theo các ví dụ minh họa và bài tập vận dụng.
Một số hữu tỉ là một số có thể được biểu diễn dưới dạng phân số a/b, trong đó a là một số nguyên và b là một số nguyên dương. a được gọi là tử số và b được gọi là mẫu số.
Mỗi số hữu tỉ đều có thể được biểu diễn trên trục số. Để biểu diễn một số hữu tỉ a/b, ta chia đoạn đơn vị trên trục số thành b phần bằng nhau, rồi đếm từ điểm gốc đến điểm thứ a.
Ví dụ: Để biểu diễn số 2/3 trên trục số, ta chia đoạn đơn vị thành 3 phần bằng nhau, rồi đếm đến điểm thứ 2.
Có nhiều cách để so sánh hai số hữu tỉ:
Ví dụ: So sánh 1/2 và 2/3.
Các phép toán cộng, trừ, nhân, chia đều có thể thực hiện trên tập hợp các số hữu tỉ. Để thực hiện các phép toán này, ta cần quy đồng mẫu số (đối với phép cộng và trừ) hoặc thực hiện phép nhân và chia phân số theo quy tắc đã học.
Ví dụ:
| Phép toán | Ví dụ | Kết quả |
|---|---|---|
| Cộng | 1/2 + 1/3 | 5/6 |
| Trừ | 2/3 - 1/4 | 5/12 |
| Nhân | 3/4 * 2/5 | 3/10 |
| Chia | 1/2 : 1/3 | 3/2 |
Bài 1: Điền vào chỗ trống:
Bài 2: Thực hiện các phép tính sau:
Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về lý thuyết tập hợp các số hữu tỉ trong chương trình Toán 7 - Kết nối tri thức. Hãy luyện tập thường xuyên để nắm vững kiến thức và tự tin giải các bài tập!