Bài học về 'Trường hợp bằng nhau của tam giác vuông' là một phần quan trọng trong chương trình Toán 7 - Kết nối tri thức. Nắm vững lý thuyết này giúp học sinh giải quyết các bài toán liên quan đến tam giác vuông một cách hiệu quả.
Tại giaitoan.edu.vn, chúng tôi cung cấp tài liệu học tập đầy đủ, dễ hiểu, giúp bạn tiếp thu kiến thức một cách nhanh chóng và hiệu quả.
1. Ba trường hợp bằng nhau của tam giác vuông
1. Ba trường hợp bằng nhau của tam giác vuông
a)Nếu 2 cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau. ( c.g.c)
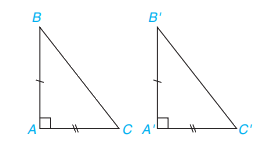
Xét tam giác ABC và A’B’C’, ta có:
AB = A’B’
\(\widehat A = \widehat {A'}( = 90^\circ )\)
AC = A’C’
Vậy \(\Delta ABC = \Delta A'B'C'\) ( c.g.c)
b) Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau. (g.c.g)
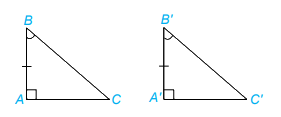
Xét tam giác ABC và A’B’C’, ta có:
\(\widehat A = \widehat {A'}( = 90^\circ )\)
AB = A’B’
\(\widehat B = \widehat {B'}\)
Vậy \(\Delta ABC = \Delta A'B'C'\) ( g.c.g)
c) Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau. ( cạnh huyền – góc nhọn)
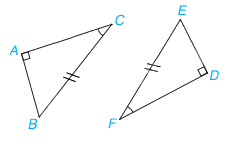
Xét tam giác vuông ABC và DEF, ta có:
BC = EF
\(\widehat C = \widehat F\)
Vậy \(\Delta ABC = \Delta DEF\) (cạnh huyền – góc nhọn)
2. Trường hợp bằng nhau đặc biệt của tam giác vuông
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau. ( cạnh huyền – cạnh góc vuông)
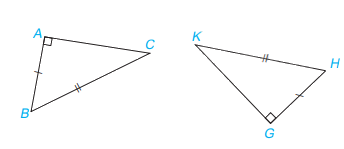
Xét tam giác vuông ABC và GHK, ta có:
BC = HK
AB = GH
Vậy \(\Delta ABC = \Delta GHK\) ( cạnh huyền – cạnh góc vuông)
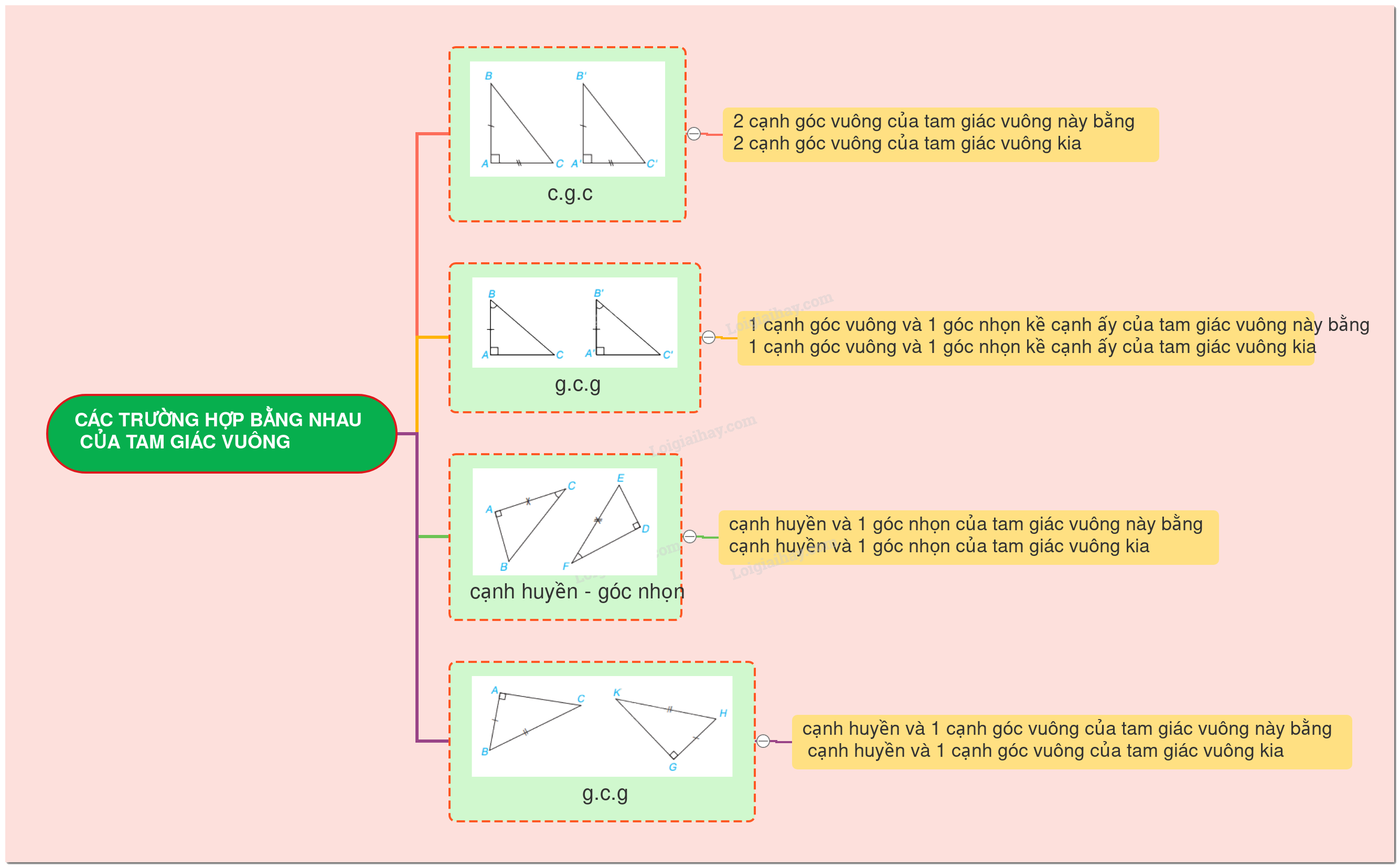
Trong hình học, việc chứng minh hai tam giác bằng nhau là một kỹ năng cơ bản và quan trọng. Đối với tam giác vuông, có những trường hợp bằng nhau đặc biệt giúp chúng ta đơn giản hóa quá trình chứng minh. Bài viết này sẽ trình bày chi tiết về lý thuyết Trường hợp bằng nhau của tam giác vuông, áp dụng trong chương trình Toán 7 - Kết nối tri thức.
Trước khi đi sâu vào tam giác vuông, chúng ta cần ôn lại các trường hợp bằng nhau của hai tam giác bất kỳ:
Ngoài ba trường hợp chung, tam giác vuông có thêm những trường hợp bằng nhau đặc biệt:
Ví dụ 1: Cho tam giác ABC vuông tại A và tam giác DEF vuông tại D, biết AB = DE, AC = DF. Chứng minh tam giác ABC = tam giác DEF.
Giải:
Xét tam giác ABC và tam giác DEF, ta có:
Vậy, tam giác ABC = tam giác DEF (trường hợp cạnh góc vuông - cạnh góc vuông).
Ví dụ 2: Cho tam giác PQR vuông tại P và tam giác XYZ vuông tại X, biết PQ = XY và ∠Q = ∠Y. Chứng minh tam giác PQR = tam giác XYZ.
Giải:
Xét tam giác PQR và tam giác XYZ, ta có:
Vậy, tam giác PQR = tam giác XYZ (trường hợp cạnh góc vuông - góc nhọn).
Để củng cố kiến thức, bạn có thể thực hành với các bài tập sau:
Lý thuyết về các trường hợp bằng nhau của tam giác vuông là một công cụ quan trọng trong việc giải các bài toán hình học. Việc nắm vững các trường hợp này giúp học sinh chứng minh hai tam giác vuông bằng nhau một cách nhanh chóng và chính xác. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích và giúp bạn tự tin hơn trong việc học tập môn Toán.