Bài học về Lý thuyết Tổng các góc trong một tam giác là một trong những kiến thức cơ bản và quan trọng trong chương trình Toán 7 - Kết nối tri thức. Việc nắm vững lý thuyết này không chỉ giúp học sinh giải quyết các bài tập trong sách giáo khoa mà còn là nền tảng cho các kiến thức hình học nâng cao hơn.
Tại giaitoan.edu.vn, chúng tôi cung cấp bài giảng chi tiết, dễ hiểu cùng với các bài tập vận dụng đa dạng để giúp bạn hiểu sâu sắc về lý thuyết này.
1. Định lí tổng 3 góc của tam giác
1. Định lí tổng 3 góc của tam giác
Tổng các góc của một tam giác bằng 180 độ.
Chú ý: + Tam giác có ba góc đều nhọn gọi là tam giác nhọn
+ Tam giác có 1 góc tù gọi là tam giác tù
+ Tam giác có 1 góc vuông gọi là tam giác vuông
Ví dụ:
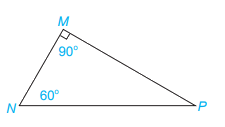
Tam giác MNP vuông tại M có:
- 2 cạnh MN và MP là 2 cạnh góc vuông, cạnh NP là cạnh huyền
- 2 góc nhọn có tổng số đo là 90 độ
2. Góc ngoài tam giác
Góc ngoài tam giác là góc kề bù với một góc trong tam giác.
Ví dụ:
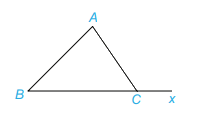
Góc ACx là góc ngoài tại C của tam giác ABC.
Tính chất:
Góc ngoài của một tam giác có số đo bằng tổng số đo của hai góc trong không kề với nó.
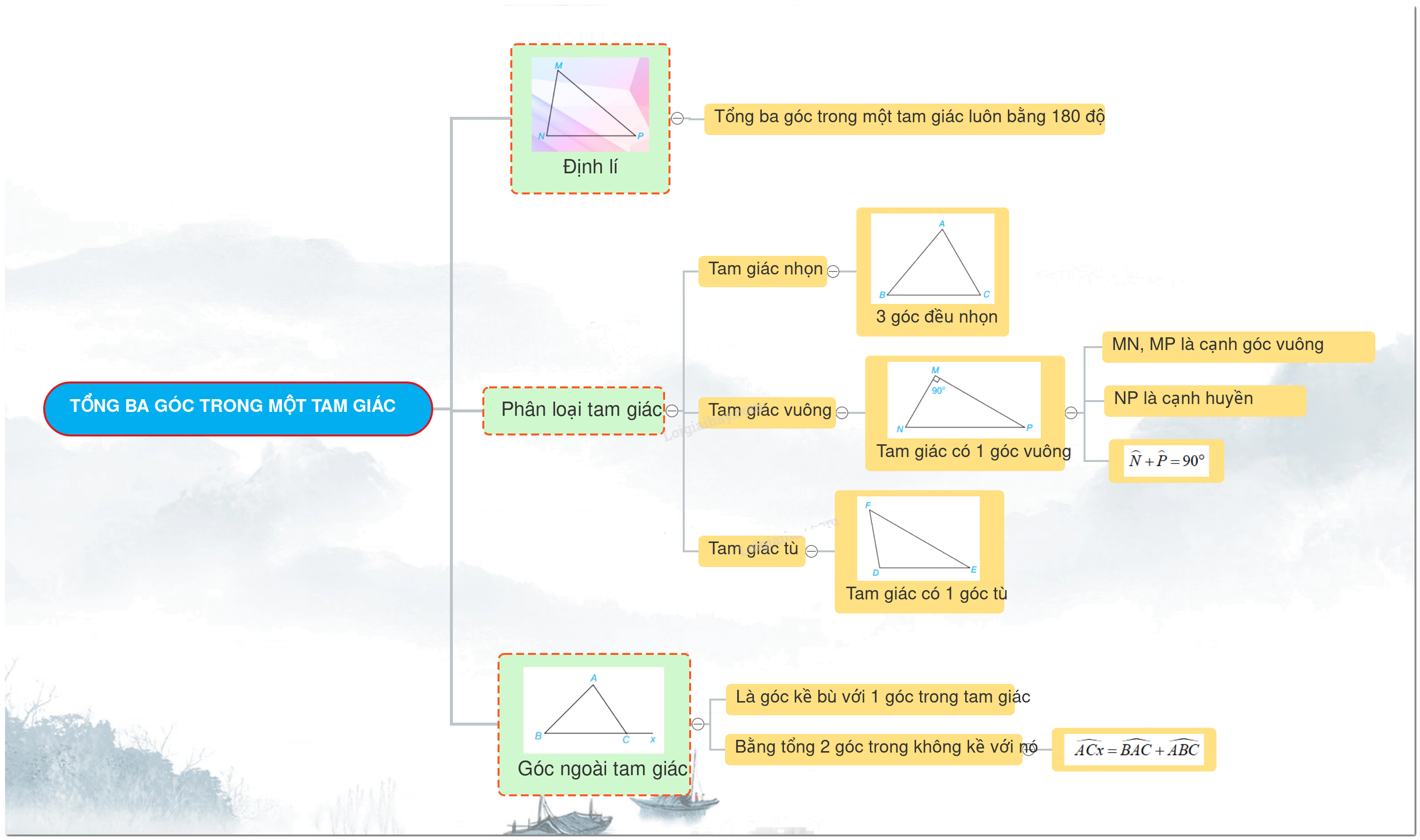
Trong hình học, tam giác là một hình đa giác có ba cạnh và ba góc. Một trong những tính chất quan trọng nhất của tam giác là tổng các góc trong của nó luôn bằng 180 độ. Đây là lý thuyết nền tảng mà học sinh lớp 7 cần nắm vững trong chương trình Toán 7 - Kết nối tri thức.
Tổng ba góc trong một tam giác bằng 180 độ. Ký hiệu: ∠A + ∠B + ∠C = 180° (với ∠A, ∠B, ∠C là các góc của tam giác ABC).
Có nhiều cách để chứng minh lý thuyết này. Một cách phổ biến là vẽ một đường thẳng song song với một cạnh của tam giác qua đỉnh đối diện. Sau đó, sử dụng các tính chất của góc so le trong và góc trong cùng phía bằng nhau để suy ra tổng ba góc trong tam giác bằng 180 độ.
Ví dụ 1: Cho tam giác ABC có ∠A = 60°, ∠B = 80°. Tính ∠C.
Giải:
Áp dụng lý thuyết tổng các góc trong một tam giác, ta có:
∠C = 180° - ∠A - ∠B = 180° - 60° - 80° = 40°
Ví dụ 2: Tam giác ABC cân tại A, ∠A = 50°. Tính các góc B và C.
Giải:
Vì tam giác ABC cân tại A nên ∠B = ∠C.
Áp dụng lý thuyết tổng các góc trong một tam giác, ta có:
∠B + ∠C = 180° - ∠A = 180° - 50° = 130°
Suy ra ∠B = ∠C = 130° / 2 = 65°
Lý thuyết tổng các góc trong một tam giác có nhiều ứng dụng trong thực tế và trong các bài toán hình học khác. Ví dụ, nó được sử dụng để tính các góc trong các hình phức tạp hơn, để chứng minh các tính chất của các loại tam giác đặc biệt (tam giác vuông, tam giác cân, tam giác đều), và để giải các bài toán liên quan đến đường cao, đường trung tuyến, đường phân giác của tam giác.
Lý thuyết Tổng các góc trong một tam giác là một kiến thức cơ bản nhưng vô cùng quan trọng trong chương trình Toán 7 - Kết nối tri thức. Việc nắm vững lý thuyết này sẽ giúp bạn tự tin hơn khi giải các bài tập hình học và xây dựng nền tảng vững chắc cho các kiến thức nâng cao hơn. Hãy luyện tập thường xuyên để hiểu sâu sắc và vận dụng linh hoạt lý thuyết này trong các tình huống khác nhau.