Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 7 tập 1 - Kết nối tri thức tại giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong SGK, giúp các em nắm vững kiến thức và tự tin hơn trong học tập.
Mục 2 của chương trình Toán 7 tập 1 tập trung vào các kiến thức cơ bản về số nguyên, phép toán trên số nguyên và các tính chất quan trọng. Việc giải bài tập một cách chính xác và hiểu rõ bản chất là điều cần thiết để xây dựng nền tảng vững chắc cho các kiến thức tiếp theo.
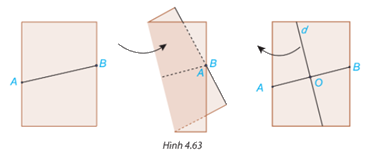
Đánh dấu hai điểm A và B nằm trên hai mép tờ giấy A4, nối A và B để được đoạn thẳng AB. Gấp mảnh giấy lại như Hình 4.63 sao cho vị trí các điểm A và B trùng nhau. Mở mảnh giấy ra, kẻ một đường thẳng d theo nếp gấp. a) Gọi O là giao điểm của đường thẳng d và AB. O có là trung điểm của đoạn thẳng AB không? b) Dùng thước đo góc, kiểm tra đường thẳng d có vuông góc với AB không?
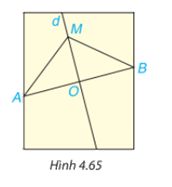
Trên mảnh giấy trong HĐ3, lấy điểm M bất kì trên đường thẳng d. Dùng thước thẳng có vạch chia kiểm tra xem AM có bằng BM không (H.4.65).
Phương pháp giải:
Dùng thước kiểm tra
Lời giải chi tiết:
Lấy điểm M bất kì trên đường thẳng d dùng thước kiểm tra ta thấy AM bằng BM.
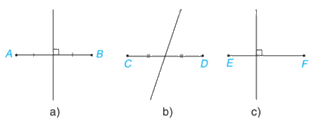
Trong Hình 4.64, bạn Lan vẽ đường trung trực của các đoạn thẳng. Theo em, hình nào Lan vẽ đúng?
Phương pháp giải:
Đường thẳng vuông góc với một đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng đó
Lời giải chi tiết:
Do: Đường thẳng vuông góc với một đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng đó
Nên hình a) Lan vẽ đúng.
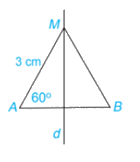
Cho M là một điểm nằm trên đường trung trực của đoạn thẳng AB. Biết AM = 3 cm và \(\widehat {MAB}\)= 60° (H.4.67). Tính BM và số đo góc MBA.
Phương pháp giải:
Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.
Lời giải chi tiết:
Vì M là một điểm nằm trên đường trung trực của đoạn thẳng AB nên MA=MB=3cm.
\(\Rightarrow\) Tam giác MAB cân tại M.
\(\Rightarrow\) \(\widehat {MAB} = \widehat {MBA} = {60^o}\).
Đánh dấu hai điểm A và B nằm trên hai mép tờ giấy A4, nối A và B để được đoạn thẳng AB.
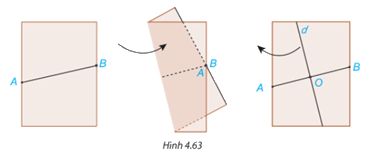
Gấp mảnh giấy lại như Hình 4.63 sao cho vị trí các điểm A và B trùng nhau. Mở mảnh giấy ra, kẻ một đường thẳng d theo nếp gấp.
a) Gọi O là giao điểm của đường thẳng d và AB. O có là trung điểm của đoạn thẳng AB không?
b) Dùng thước đo góc, kiểm tra đường thẳng d có vuông góc với AB không?
Phương pháp giải:
Dùng thước đo kiểm tra.
Lời giải chi tiết:
a) O có là trung điểm của đoạn thẳng AB
b) Dùng thước đo góc ta thấy d có vuông góc với AB.
Đánh dấu hai điểm A và B nằm trên hai mép tờ giấy A4, nối A và B để được đoạn thẳng AB.
Gấp mảnh giấy lại như Hình 4.63 sao cho vị trí các điểm A và B trùng nhau. Mở mảnh giấy ra, kẻ một đường thẳng d theo nếp gấp.
a) Gọi O là giao điểm của đường thẳng d và AB. O có là trung điểm của đoạn thẳng AB không?
b) Dùng thước đo góc, kiểm tra đường thẳng d có vuông góc với AB không?
Phương pháp giải:
Dùng thước đo kiểm tra.
Lời giải chi tiết:
a) O có là trung điểm của đoạn thẳng AB
b) Dùng thước đo góc ta thấy d có vuông góc với AB.
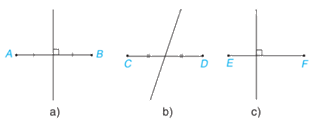
Trong Hình 4.64, bạn Lan vẽ đường trung trực của các đoạn thẳng. Theo em, hình nào Lan vẽ đúng?
Phương pháp giải:
Đường thẳng vuông góc với một đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng đó
Lời giải chi tiết:
Do: Đường thẳng vuông góc với một đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng đó
Nên hình a) Lan vẽ đúng.
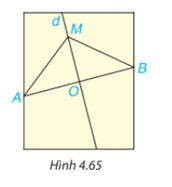
Trên mảnh giấy trong HĐ3, lấy điểm M bất kì trên đường thẳng d. Dùng thước thẳng có vạch chia kiểm tra xem AM có bằng BM không (H.4.65).
Phương pháp giải:
Dùng thước kiểm tra
Lời giải chi tiết:
Lấy điểm M bất kì trên đường thẳng d dùng thước kiểm tra ta thấy AM bằng BM.
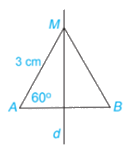
Cho M là một điểm nằm trên đường trung trực của đoạn thẳng AB. Biết AM = 3 cm và \(\widehat {MAB}\)= 60° (H.4.67). Tính BM và số đo góc MBA.
Phương pháp giải:
Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.
Lời giải chi tiết:
Vì M là một điểm nằm trên đường trung trực của đoạn thẳng AB nên MA=MB=3cm.
\(\Rightarrow\) Tam giác MAB cân tại M.
\(\Rightarrow\) \(\widehat {MAB} = \widehat {MBA} = {60^o}\).
Mục 2 trong SGK Toán 7 tập 1 - Kết nối tri thức là một phần quan trọng, đặt nền móng cho việc hiểu và vận dụng các kiến thức về số nguyên. Nội dung chính của mục này bao gồm các khái niệm về số nguyên âm, số nguyên dương, số 0, trục số, và các phép toán cơ bản trên số nguyên như cộng, trừ, nhân, chia. Việc nắm vững các khái niệm này là điều kiện tiên quyết để giải quyết các bài tập một cách hiệu quả.
Trang 81 SGK Toán 7 tập 1 - Kết nối tri thức thường chứa các bài tập vận dụng các kiến thức cơ bản về số nguyên âm, số nguyên dương và số 0. Các bài tập này thường yêu cầu học sinh:
Ví dụ, bài tập 1 trang 81 có thể yêu cầu học sinh biểu diễn các số -3, 2, 0 trên trục số. Để giải bài tập này, học sinh cần xác định vị trí của các số trên trục số, với số 0 là điểm gốc, các số dương nằm bên phải và các số âm nằm bên trái.
Trang 82 thường tập trung vào các bài tập về phép cộng, trừ số nguyên. Các bài tập này có thể yêu cầu học sinh:
Ví dụ, bài tập 2 trang 82 có thể yêu cầu học sinh tính (-5) + 3. Để giải bài tập này, học sinh cần áp dụng quy tắc cộng hai số nguyên khác dấu: cộng các giá trị tuyệt đối và giữ dấu của số có giá trị tuyệt đối lớn hơn. Trong trường hợp này, (-5) + 3 = -2.
Trang 83 thường chứa các bài tập tổng hợp, yêu cầu học sinh vận dụng nhiều kiến thức khác nhau về số nguyên. Các bài tập này có thể yêu cầu học sinh:
Ví dụ, bài tập 3 trang 83 có thể yêu cầu học sinh tính 2 - (-4) + (-1). Để giải bài tập này, học sinh cần áp dụng quy tắc trừ hai số nguyên và quy tắc cộng hai số nguyên khác dấu. 2 - (-4) + (-1) = 2 + 4 - 1 = 5.
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin hơn trong việc giải các bài tập mục 2 trang 81, 82, 83 SGK Toán 7 tập 1 - Kết nối tri thức. Chúc các em học tập tốt!