Bài 4.12 trang 73 SGK Toán 7 tập 1 thuộc chương trình Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về biểu thức đại số và tính giá trị của biểu thức. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.12 trang 73 SGK Toán 7 tập 1, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Trong mỗi hình bên (H.4.39), hãy chỉ ra một cặp tam giác bằng nhau và giải thích vì sao chúng bằng nhau.
Đề bài
Trong mỗi hình bên (H.4.39), hãy chỉ ra một cặp tam giác bằng nhau và giải thích vì sao chúng bằng nhau.
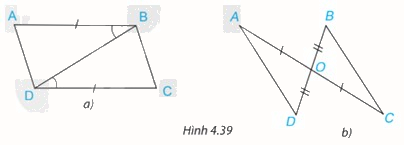
Phương pháp giải - Xem chi tiết
Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
Lời giải chi tiết
a)Xét \(\Delta ABD\) và \(\Delta CDB\) có:
AB=CD (gt)
\(\widehat {ABD} = \widehat {CDB}\) (gt)
BD chung
Vậy \(\Delta ABD = \Delta CDB\)(c.g.c)
b)Xét \(\Delta OAD\) và \(\Delta OCB\) có:
AO=CO (gt)
\(\widehat {AOD} = \widehat {COB}\) (đối đỉnh)
OD=OB (gt)
Vậy \(\Delta OAD = \Delta OCB\)(c.g.c)
Bài 4.12 trang 73 SGK Toán 7 tập 1 - Kết nối tri thức yêu cầu chúng ta tìm giá trị của biểu thức đại số. Để giải bài này, chúng ta cần nắm vững các quy tắc về thứ tự thực hiện các phép toán, các tính chất của phép cộng, trừ, nhân, chia và các quy tắc về dấu ngoặc.
Tính giá trị của các biểu thức sau:
Để tính giá trị của biểu thức, ta thay giá trị của biến vào biểu thức và thực hiện các phép toán theo đúng thứ tự.
Thay x = 2 vào biểu thức, ta được:
3 * 2 + 5 = 6 + 5 = 11
Vậy, giá trị của biểu thức 3x + 5 với x = 2 là 11.
Thay y = -1 vào biểu thức, ta được:
7 * (-1) - 4 = -7 - 4 = -11
Vậy, giá trị của biểu thức 7y - 4 với y = -1 là -11.
Thay z = 3 vào biểu thức, ta được:
2 * 32 + 1 = 2 * 9 + 1 = 18 + 1 = 19
Vậy, giá trị của biểu thức 2z2 + 1 với z = 3 là 19.
Thay a = 1 và b = -2 vào biểu thức, ta được:
5 * 1 - 3 * (-2) = 5 + 6 = 11
Vậy, giá trị của biểu thức 5a - 3b với a = 1 và b = -2 là 11.
Để củng cố kiến thức, các em có thể tự giải các bài tập tương tự sau:
Bài 4.12 trang 73 SGK Toán 7 tập 1 - Kết nối tri thức là một bài tập cơ bản giúp học sinh làm quen với việc tính giá trị của biểu thức đại số. Việc nắm vững các quy tắc và tính chất của các phép toán là rất quan trọng để giải quyết bài tập này một cách chính xác và hiệu quả. Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em học sinh sẽ tự tin hơn trong việc học tập môn Toán.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!