Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng về mối quan hệ giữa đường vuông góc, đường xiên và hình chiếu trong hình học lớp 7. Chúng ta sẽ cùng nhau khám phá các định nghĩa, tính chất và ứng dụng của các khái niệm này.
Nắm vững lý thuyết này là nền tảng để giải quyết các bài toán liên quan đến tam giác vuông, góc và khoảng cách trong không gian. Giaitoan.edu.vn sẽ giúp bạn hiểu rõ và áp dụng kiến thức một cách hiệu quả.
Khái niệm về đường vuông góc, đường xiên và hình chiếu của đường xiên
1. Khái niệm về đường vuông góc, đường xiên và hình chiếu của đường xiên
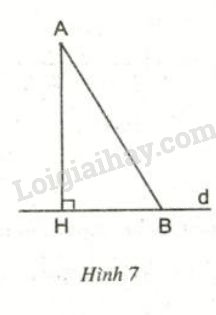
Từ \(A\) không nằm trên \(d\), kẻ một đường thẳng vuông góc với \(d\) tại \(H\). Trên \(d\) lấy điểm \(B\) không trùng với \(H\). Khi đó:
+ Đoạn \(AH\) gọi là đoạn vuông góc hay đường vuông góc kẻ từ \(A\) đến \(d\).
+ Đoạn \(AB\) gọi là đường xiên kẻ từ \(A\) đến \(d\)
+ Đoạn \(HB\) gọi là hình chiếu của đường xiên \(AB\) lên đường thẳng \(d\).
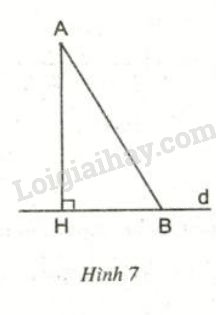
2. Quan hệ giữa đường vuông góc và đường xiên
Định lý 1: Trong các đường xiên và đường vuông góc kẻ từ một điểm ở ngoài một đường thẳng đến đường thẳng đó, đường vuông góc là đường ngắn nhất.
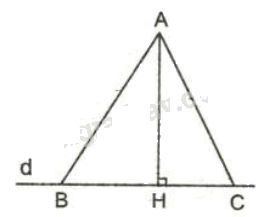
3. Quan hệ giữa các đường xiên và hình chiếu của chúng
Định lý 2: Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó;
a) Đường xiên nào có hình chiếu lớn hơn thì lớn hơn
b) Đường xiên nào lớn hơn thì có hình chiếu lớn hơn
c) Nếu hai đường xiên bằng nhau thì hai hình chiếu bằng nhau và ngược lại nếu hai hình chiếu bằng nhau thì hai đường xiên bằng nhau.
4. Các dạng toán thường gặp
Dạng 1: Chỉ ra hai đường xiên bằng nhau hoặc hai hình chiếu bằng nhau
Phương pháp:
Ta sử dụng: “Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó: nếu hai đường xiên bằng nhau thì hai hình chiếu bằng nhau; nếu hai hình chiếu bằng nhau thì hai đường xiên bằng nhau.”
Dạng 2: So sánh hai đường xiên hoặc hai hình chiếu
Phương pháp:
Ta sử dụng định lý:
Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó:
+ Đường xiên nào có hình chiếu lớn hơn thì lớn hơn
+ Đường xiên nào lớn hơn thì có hình chiếu lớn hơn
+ Nếu hai đường xiên bằng nhau thì hai hình chiếu bằng nhau; nếu hai hình chiếu bằng nhau thì hai đường xiên bằng nhau.
Dạng 3: Quan hệ giữa đường vuông góc và đường xiên
Phương pháp:
Ta sử dụng định lý:
Trong các đường vuông góc và đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó, đường vuông góc ngắn hơn mọi đường xiên.
Trong hình học lớp 7, việc hiểu rõ mối quan hệ giữa đường vuông góc, đường xiên và hình chiếu là vô cùng quan trọng. Bài viết này sẽ trình bày chi tiết lý thuyết này, kèm theo các ví dụ minh họa và bài tập thực hành để giúp bạn nắm vững kiến thức.
Đường vuông góc: Là đường thẳng tạo với đường thẳng khác một góc vuông (90 độ). Nếu AB vuông góc với CD, ta ký hiệu AB ⊥ CD.
Đường xiên: Là đường thẳng không vuông góc với đường thẳng khác và cắt đường thẳng đó. Đường xiên tạo với đường thẳng đó một góc nhọn hoặc góc tù.
Hình chiếu của một điểm trên một đường thẳng: Hình chiếu của điểm A trên đường thẳng d là điểm H sao cho AH vuông góc với d.
Hình chiếu của một đoạn thẳng trên một đường thẳng: Hình chiếu của đoạn thẳng AB trên đường thẳng d là đoạn thẳng A'B' trong đó A' và B' là hình chiếu của A và B trên d.
Trong một tam giác vuông, đường vuông góc kẻ từ đỉnh góc vuông xuống cạnh huyền là đường cao. Đường cao này chia tam giác vuông thành hai tam giác vuông nhỏ hơn, đồng dạng với tam giác vuông ban đầu và đồng dạng với nhau.
Định lý 1: Trong một tam giác vuông, đường vuông góc kẻ từ đỉnh góc vuông xuống cạnh huyền ngắn hơn bất kỳ đường xiên nào kẻ từ đỉnh đó đến cạnh huyền.
Chứng minh: (Chứng minh dựa trên bất đẳng thức tam giác và tính chất của tam giác vuông)
Định lý 2: Trong một tam giác vuông, đường xiên nào lớn hơn thì hình chiếu của nó trên cạnh huyền cũng lớn hơn.
Chứng minh: (Chứng minh dựa trên các tam giác đồng dạng và tỉ lệ thức)
Lý thuyết về đường vuông góc, đường xiên và hình chiếu được ứng dụng rộng rãi trong việc giải các bài toán hình học, đặc biệt là các bài toán liên quan đến tam giác vuông, góc và khoảng cách.
Bài 1: Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 6cm, AC = 8cm. Tính độ dài AH.
Bài 2: Cho tam giác ABC vuông tại A, đường cao AH. Biết BH = 4cm, CH = 9cm. Tính độ dài AB và AC.
Bài 3: Cho tam giác ABC vuông tại A, đường cao AH. Gọi D và E lần lượt là hình chiếu của H trên AB và AC. Chứng minh rằng ADHE là hình chữ nhật.
Lý thuyết về quan hệ giữa đường vuông góc, đường xiên và hình chiếu là một phần quan trọng của chương trình hình học lớp 7. Việc nắm vững lý thuyết này sẽ giúp bạn giải quyết các bài toán một cách dễ dàng và hiệu quả hơn. Hãy luyện tập thường xuyên để củng cố kiến thức và rèn luyện kỹ năng giải toán.
| Khái niệm | Định nghĩa |
|---|---|
| Đường vuông góc | Đường thẳng tạo với đường thẳng khác một góc vuông. |
| Đường xiên | Đường thẳng không vuông góc với đường thẳng khác và cắt đường thẳng đó. |
| Hình chiếu | Hình chiếu của một điểm (hoặc đoạn thẳng) trên một đường thẳng là điểm (hoặc đoạn thẳng) sao cho đường nối điểm (hoặc các đầu mút đoạn thẳng) với hình chiếu vuông góc với đường thẳng đó. |