Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 7 Kết Nối Tri Thức trang 26, 27, 28 của giaitoan.edu.vn. Chúng tôi cung cấp đáp án và lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập Toán 7.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi cam kết mang đến cho các em những bài giải chính xác, khoa học và phù hợp với chương trình học.
Kết quả của phép chia 1 cho 9 là số thập phân hữu hạn hay vô hạn tuần hoàn?...Viết các phân số...
Kết quả của phép chia 1 cho 9 là số thập phân hữu hạn hay vô hạn tuần hoàn?
Phương pháp giải:
Bước 1: Chia 1 cho 9 để tìm thương dưới dạng số thập phân.
Bước 2: Nhận diện số thập phân đó là hữu hạn hay vô hạn tuần hoàn
Lời giải chi tiết:
Ta có: 1: 9 = 0,1111.... = 0,(1) nên kết quả của phép chia 1 cho 9 là số thập phân vô hạn tuần hoàn.
Viết các phân số \(\frac{1}{4}; - \frac{2}{{11}}\) dưới dạng số thập phân rồi cho biết số nhận được là số thập phân hữu hạn hay vô hạn tuần hoàn.
Chỉ ra chu kì rồi viết gọn nếu đó là số thập phân vô hạn tuần hoàn.
Phương pháp giải:
Thực hiện phép chia tử số cho mẫu số để thu được số thập phân.
Nhận diện số thập phân đó là hữu hạn hay vô hạn tuần hoàn
Lời giải chi tiết:
Ta có: \(\frac{1}{4} = 0,25\). Đây là số thập phân hữu hạn.
\( - \frac{2}{{11}} = - 0,1818....\). Đây là số thập phân vô hạn tuần hoàn. Chu kì của nó là 18. Ta viết \( - \frac{2}{{11}}=-0,(18)\)
Ước lượng kết quả phép tính 31,(81).4,9 bằng cách làm tròn hai thừa số đến hàng đơn vị.
Phương pháp giải:
+ Bước 1: Làm tròn 2 thừa số đến hàng đơn vị
+ Bước 2: Tính tích 2 thừa số sau khi làm tròn
Lời giải chi tiết:
Ta có: Làm tròn số 31,(81) đến hàng đơn vị được 32; làm tròn số 4,9 đến hàng đơn vị được 5.
Như vậy, kết quả phép tính 31,(81).4,9 ước lượng được là: 32.5 = 160.
Làm tròn số 3,14159 với độ chính xác 0,005.
Phương pháp giải:
+ Bước 1: Xác định hàng làm tròn.
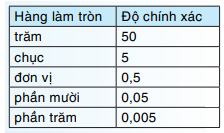
+ Bước 2: Làm tròn theo quy tắc làm tròn số thập phân.
- Đối với chữ số hàng làm tròn:
+ Giữ nguyên nếu chữ số ngay bên phải nhỏ hơn 5;
+Tăng 1 đơn vị nếu chữ số ngay bên phải lớn hơn hoặc bằng 5
- Đối với chữ số sau hàng làm tròn:
+ Bỏ đi nếu ở phần thập phân;
+ Thay bằng các chữ số 0 nếu ở phần số nguyên
Lời giải chi tiết:
Để làm tròn 3,14159 với độ chính xác 0,005, ta làm tròn đến hàng phần trăm.
Vì chữ số ngay sau phần làm tròn là 1 < 5 nên số 3,14159 làm tròn đến hàng phần trăm là: 3,14
Kết quả của phép chia 1 cho 9 là số thập phân hữu hạn hay vô hạn tuần hoàn?
Phương pháp giải:
Bước 1: Chia 1 cho 9 để tìm thương dưới dạng số thập phân.
Bước 2: Nhận diện số thập phân đó là hữu hạn hay vô hạn tuần hoàn
Lời giải chi tiết:
Ta có: 1: 9 = 0,1111.... = 0,(1) nên kết quả của phép chia 1 cho 9 là số thập phân vô hạn tuần hoàn.
Viết các phân số \(\frac{1}{4}; - \frac{2}{{11}}\) dưới dạng số thập phân rồi cho biết số nhận được là số thập phân hữu hạn hay vô hạn tuần hoàn.
Chỉ ra chu kì rồi viết gọn nếu đó là số thập phân vô hạn tuần hoàn.
Phương pháp giải:
Thực hiện phép chia tử số cho mẫu số để thu được số thập phân.
Nhận diện số thập phân đó là hữu hạn hay vô hạn tuần hoàn
Lời giải chi tiết:
Ta có: \(\frac{1}{4} = 0,25\). Đây là số thập phân hữu hạn.
\( - \frac{2}{{11}} = - 0,1818....\). Đây là số thập phân vô hạn tuần hoàn. Chu kì của nó là 18. Ta viết \( - \frac{2}{{11}}=-0,(18)\)
Làm tròn số 3,14159 với độ chính xác 0,005.
Phương pháp giải:
+ Bước 1: Xác định hàng làm tròn.
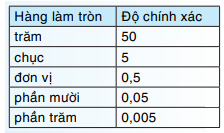
+ Bước 2: Làm tròn theo quy tắc làm tròn số thập phân.
- Đối với chữ số hàng làm tròn:
+ Giữ nguyên nếu chữ số ngay bên phải nhỏ hơn 5;
+Tăng 1 đơn vị nếu chữ số ngay bên phải lớn hơn hoặc bằng 5
- Đối với chữ số sau hàng làm tròn:
+ Bỏ đi nếu ở phần thập phân;
+ Thay bằng các chữ số 0 nếu ở phần số nguyên
Lời giải chi tiết:
Để làm tròn 3,14159 với độ chính xác 0,005, ta làm tròn đến hàng phần trăm.
Vì chữ số ngay sau phần làm tròn là 1 < 5 nên số 3,14159 làm tròn đến hàng phần trăm là: 3,14
Ước lượng kết quả phép tính 31,(81).4,9 bằng cách làm tròn hai thừa số đến hàng đơn vị.
Phương pháp giải:
+ Bước 1: Làm tròn 2 thừa số đến hàng đơn vị
+ Bước 2: Tính tích 2 thừa số sau khi làm tròn
Lời giải chi tiết:
Ta có: Làm tròn số 31,(81) đến hàng đơn vị được 32; làm tròn số 4,9 đến hàng đơn vị được 5.
Như vậy, kết quả phép tính 31,(81).4,9 ước lượng được là: 32.5 = 160.
Chương trình Toán 7 Kết Nối Tri Thức tập trung vào việc xây dựng nền tảng vững chắc về đại số và hình học. Trang 26, 27, 28 của sách giáo khoa Toán 7 tập 1 tập trung vào các chủ đề quan trọng như số hữu tỉ, phép cộng, trừ, nhân, chia số hữu tỉ, và các tính chất của các phép toán này. Việc nắm vững kiến thức này là vô cùng quan trọng cho việc học tập các kiến thức toán học nâng cao hơn trong tương lai.
Trang 26 giới thiệu các bài tập về việc nhận biết và phân loại số hữu tỉ. Các bài tập này giúp học sinh hiểu rõ hơn về khái niệm số hữu tỉ, cách biểu diễn số hữu tỉ trên trục số, và mối quan hệ giữa các số hữu tỉ. Cụ thể, các em sẽ thực hành:
Trang 27 tập trung vào việc thực hành các phép cộng và trừ số hữu tỉ. Các bài tập này yêu cầu học sinh áp dụng các quy tắc cộng, trừ số hữu tỉ để tìm ra kết quả chính xác. Các dạng bài tập thường gặp bao gồm:
Để giải các bài tập này, học sinh cần nắm vững các quy tắc sau:
Trang 28 giới thiệu các bài tập về phép nhân và chia số hữu tỉ. Các bài tập này yêu cầu học sinh áp dụng các quy tắc nhân, chia số hữu tỉ để tìm ra kết quả chính xác. Các dạng bài tập thường gặp bao gồm:
Lưu ý khi thực hiện phép nhân, chia số hữu tỉ:
Việc giải bài tập Toán 7 Kết Nối Tri Thức trang 26, 27, 28 không chỉ giúp học sinh nắm vững kiến thức mà còn rèn luyện kỹ năng giải toán, tư duy logic và khả năng áp dụng kiến thức vào thực tế. Đây là nền tảng quan trọng để học sinh có thể tiếp thu các kiến thức toán học nâng cao hơn trong các lớp học tiếp theo.
Hy vọng với những hướng dẫn chi tiết và lời giải đầy đủ trên đây, các em học sinh sẽ tự tin giải các bài tập Toán 7 Kết Nối Tri Thức trang 26, 27, 28 một cách hiệu quả. Chúc các em học tập tốt!