Bài 10.17 trang 101 SGK Toán 7 tập 2 thuộc chương trình Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng áp dụng các kiến thức về tam giác cân đã học. Bài tập này thường yêu cầu học sinh chứng minh một tính chất hoặc giải một bài toán liên quan đến tam giác cân.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 10.17 trang 101 SGK Toán 7 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Viết tên đỉnh, cạnh, mặt bên, mặt đáy của hình lăng trụ đứng tứ giác ở hình 10.40
Đề bài
Viết tên đỉnh, cạnh, mặt bên, mặt đáy của hình lăng trụ đứng tứ giác ở hình 10.40
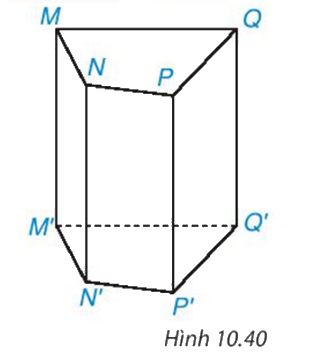
Phương pháp giải - Xem chi tiết
Áp dụng các hoạt động 1,2 học bài 37.
Lời giải chi tiết
Ta có:
+ 8 đỉnh : M, N, P, Q, M', N', P', Q'.
+ 12 cạnh : MN, MQ, NP, PQ, M'N', M'Q', N'P', P'Q', MM', NN', PP', QQ'.
+ 4 mặt bên : MNN'M', NPP'N', PQQ'P', MQQ'M'.
+ 2 mặt đáy : MNPQ, M'N'P'Q'.
Bài 10.17 SGK Toán 7 tập 2 Kết nối tri thức yêu cầu học sinh chứng minh một tính chất liên quan đến tam giác cân. Để giải bài này, chúng ta cần nắm vững các kiến thức cơ bản về tam giác cân, bao gồm định nghĩa, tính chất và các dấu hiệu nhận biết tam giác cân.
Trước khi đi vào giải bài tập, chúng ta cần đọc kỹ đề bài và xác định yêu cầu của bài toán. Thông thường, bài toán sẽ cho một hình vẽ hoặc một giả thiết nào đó liên quan đến tam giác. Nhiệm vụ của chúng ta là sử dụng các kiến thức đã học để chứng minh một kết luận nào đó.
(Nội dung lời giải chi tiết bài 10.17 sẽ được trình bày tại đây, bao gồm các bước chứng minh, giải thích rõ ràng và sử dụng các ký hiệu toán học chính xác. Lời giải sẽ được chia thành các bước nhỏ để dễ theo dõi và hiểu.)
Ví dụ, lời giải có thể bao gồm:
Ngoài bài 10.17, còn rất nhiều bài tập tương tự về tam giác cân. Để giải các bài tập này, chúng ta có thể áp dụng các phương pháp sau:
Để củng cố kiến thức về tam giác cân, các em có thể tự giải các bài tập sau:
Bài 10.17 trang 101 SGK Toán 7 tập 2 - Kết nối tri thức là một bài tập quan trọng giúp học sinh hiểu sâu hơn về tam giác cân. Hy vọng với lời giải chi tiết và các phương pháp giải đã trình bày, các em học sinh sẽ tự tin giải các bài tập tương tự và đạt kết quả tốt trong môn Toán.