Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 7 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các câu hỏi trong sách giáo khoa Toán 7 tập 2, trang 63 và 64, chương trình Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập. Hãy cùng chúng tôi khám phá lời giải cho từng bài tập nhé!
Cho điểm A không nằm trên đường thẳng d. a) Hãy vẽ đường vuông góc AH và một đường xiên AM từ A đến d. b) Em hãy giải thích vì sao AH < AM
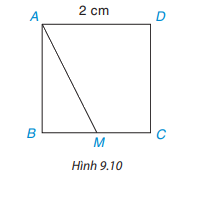
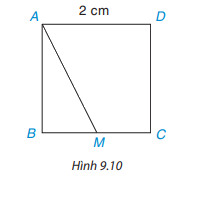
Cho hình vuông ABCD có độ dài cạnh bằng 2 cm, M là một điểm trên cạnh BC như Hình 9.10
a) Hãy chỉ ra các đường vuông góc và đường xiên kẻ từ điểm A đến đường thẳng BC.
b) So sánh hai đoạn thẳng AB và AM.
c) Tìm khoảng cách từ điểm C đến đường thẳng AB.
Phương pháp giải:
Sử dụng định lí: Trong các đường xiên và đường vuông góc kẻ từ 1 điểm nằm ngoài 1 đường thẳng đến đường thẳng đó thì đường vuông góc là đường ngắn nhất.
Lời giải chi tiết:
a) Đường vuông góc kẻ từ A đến BC là: AB
Đường xiên kẻ từ A đến BC là: AM
b) AB < AM (Trong các đường xiên và đường vuông góc kẻ từ 1 điểm nằm ngoài 1 đường thẳng đến đường thẳng đó thì đường vuông góc là đường ngắn nhất.)
c) Vì CB \( \bot \) AB nên khoảng cách từ C đến AB là độ dài CB = 2 cm
Cho điểm A không nằm trên đường thẳng d.
a) Hãy vẽ đường vuông góc AH và một đường xiên AM từ A đến d.
b) Em hãy giải thích vì sao AH < AM
Phương pháp giải:
Áp dụng: Trong 1 tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
Lời giải chi tiết:
a)
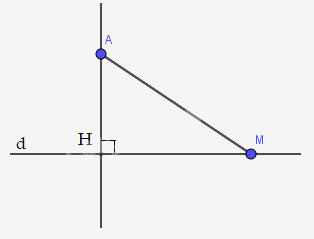
b) Trong tam giác AHM có \(\widehat {AHM} = 90^\circ \) nên là góc lớn nhất trong tam giác.
Cạnh AM đối diện với góc AHM nên là cạnh lớn nhất ( trong 1 tam giác, cạnh đối diện với góc lớn nhất là cạnh lớn nhất)
\( \Rightarrow AM > AH\)
Vậy AH < AM
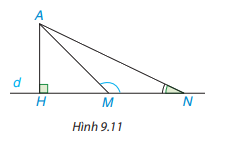
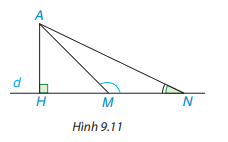
a) Quan sát hình 9.11, ta thấy khi M thay đổi trên d, M càng xa H thì AM càng lớn lên, tức là nếu HM < HN thì AM < AN. Hãy chứng minh khẳng định này nhờ quan hệ giữa góc và cạnh đối diện trong tam giác AMN.
b) Xét hình vuông ABCD và một điểm M tùy ý nằm trên các cạnh của hình vuông. Hỏi với vị trí nào của M thì AM lớn nhất? Vì sao?
Phương pháp giải:
Sử dụng định lí: Trong một tam giác, cạnh đối diện với góc lớn nhất là cạnh lớn nhất.
Lời giải chi tiết:
+) TH1:
M nằm giữa H và N:
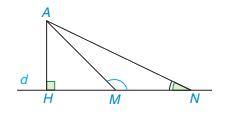
Vì góc AMN là góc ngoài tại đỉnh M của tam giác AHM nên \(\widehat{AMN} = \widehat{MAH} + \widehat{AHM} > \widehat{AHM} = 90^0\) hay \(\widehat{AMN}\) là góc tù.
Xét tam giác AMN có \(\widehat{AMN}\) là góc tù nên là góc lớn nhất trong tam giác. Cạnh AN đối diện với \(\widehat{AMN}\) nên là cạnh lớn nhất trong tam giác (định lí)
Vậy AM < AN
+) TH2:
H nằm giữa M và N:
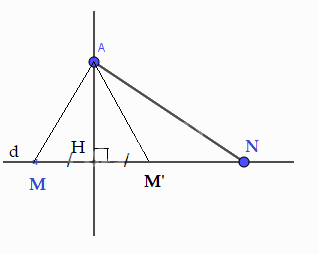
Lấy điểm M’ trên d sao cho HM’ = HM. Ta được AH là đường trung trực của đoạn thẳng MM’ nên AM = AM’ ( tính chất đường trung trực của đoạn thẳng)
Hơn nữa, AM’ < AN ( theo trường hợp 1)
AM < AN
Vậy AM < AN.
b)
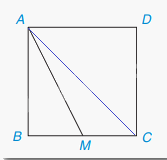
Theo câu a, khi M thay đổi trên BC, M càng xa B thì AM càng lớn. Khi M trùng C thì M xa B nhất nên khi đó AM là lớn nhất.
Tình huống mở đầu
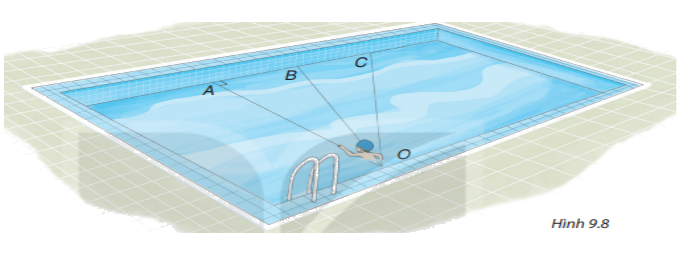
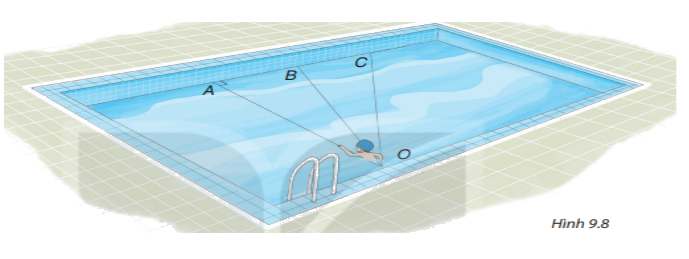
Bạn Nam tập bơi ở một bể bơi hình chữ nhật, trong đó có ba đường bơi OA, OB, OC. Biết rằng OA vuông góc với cạnh của bể bơi (H.9.8)
Nếu xuất phát từ điểm O và bơi cùng tốc độ, để bơi sang bờ bên kia nhanh nhất thì bạn Nam nên chọn đường bơi nào?
Phương pháp giải:
Sử dụng định lí: Trong các đường xiên và đường vuông góc kẻ từ 1 điểm nằm ngoài 1 đường thẳng đến đường thẳng đó thì đường vuông góc là đường ngắn nhất.
Lời giải chi tiết:
Trong các đường xiên và đường vuông góc kẻ từ O đến bờ bên kia của bể bơi thì OA là đường vuôn góc nên ngắn nhất ( Định lí)
Cho điểm A không nằm trên đường thẳng d.
a) Hãy vẽ đường vuông góc AH và một đường xiên AM từ A đến d.
b) Em hãy giải thích vì sao AH < AM
Phương pháp giải:
Áp dụng: Trong 1 tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
Lời giải chi tiết:
a)
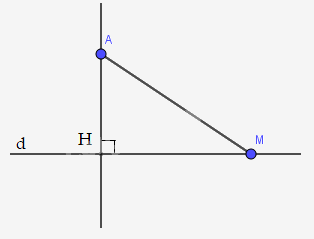
b) Trong tam giác AHM có \(\widehat {AHM} = 90^\circ \) nên là góc lớn nhất trong tam giác.
Cạnh AM đối diện với góc AHM nên là cạnh lớn nhất ( trong 1 tam giác, cạnh đối diện với góc lớn nhất là cạnh lớn nhất)
\( \Rightarrow AM > AH\)
Vậy AH < AM
Cho hình vuông ABCD có độ dài cạnh bằng 2 cm, M là một điểm trên cạnh BC như Hình 9.10
a) Hãy chỉ ra các đường vuông góc và đường xiên kẻ từ điểm A đến đường thẳng BC.
b) So sánh hai đoạn thẳng AB và AM.
c) Tìm khoảng cách từ điểm C đến đường thẳng AB.
Phương pháp giải:
Sử dụng định lí: Trong các đường xiên và đường vuông góc kẻ từ 1 điểm nằm ngoài 1 đường thẳng đến đường thẳng đó thì đường vuông góc là đường ngắn nhất.
Lời giải chi tiết:
a) Đường vuông góc kẻ từ A đến BC là: AB
Đường xiên kẻ từ A đến BC là: AM
b) AB < AM (Trong các đường xiên và đường vuông góc kẻ từ 1 điểm nằm ngoài 1 đường thẳng đến đường thẳng đó thì đường vuông góc là đường ngắn nhất.)
c) Vì CB \( \bot \) AB nên khoảng cách từ C đến AB là độ dài CB = 2 cm
Tình huống mở đầu
Bạn Nam tập bơi ở một bể bơi hình chữ nhật, trong đó có ba đường bơi OA, OB, OC. Biết rằng OA vuông góc với cạnh của bể bơi (H.9.8)
Nếu xuất phát từ điểm O và bơi cùng tốc độ, để bơi sang bờ bên kia nhanh nhất thì bạn Nam nên chọn đường bơi nào?
Phương pháp giải:
Sử dụng định lí: Trong các đường xiên và đường vuông góc kẻ từ 1 điểm nằm ngoài 1 đường thẳng đến đường thẳng đó thì đường vuông góc là đường ngắn nhất.
Lời giải chi tiết:
Trong các đường xiên và đường vuông góc kẻ từ O đến bờ bên kia của bể bơi thì OA là đường vuôn góc nên ngắn nhất ( Định lí)
a) Quan sát hình 9.11, ta thấy khi M thay đổi trên d, M càng xa H thì AM càng lớn lên, tức là nếu HM < HN thì AM < AN. Hãy chứng minh khẳng định này nhờ quan hệ giữa góc và cạnh đối diện trong tam giác AMN.
b) Xét hình vuông ABCD và một điểm M tùy ý nằm trên các cạnh của hình vuông. Hỏi với vị trí nào của M thì AM lớn nhất? Vì sao?
Phương pháp giải:
Sử dụng định lí: Trong một tam giác, cạnh đối diện với góc lớn nhất là cạnh lớn nhất.
Lời giải chi tiết:
+) TH1:
M nằm giữa H và N:
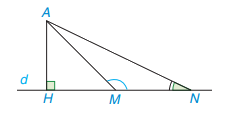
Vì góc AMN là góc ngoài tại đỉnh M của tam giác AHM nên \(\widehat{AMN} = \widehat{MAH} + \widehat{AHM} > \widehat{AHM} = 90^0\) hay \(\widehat{AMN}\) là góc tù.
Xét tam giác AMN có \(\widehat{AMN}\) là góc tù nên là góc lớn nhất trong tam giác. Cạnh AN đối diện với \(\widehat{AMN}\) nên là cạnh lớn nhất trong tam giác (định lí)
Vậy AM < AN
+) TH2:
H nằm giữa M và N:
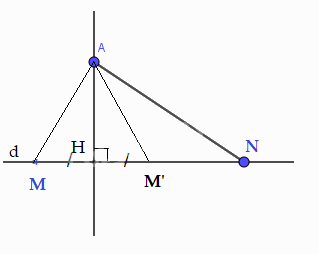
Lấy điểm M’ trên d sao cho HM’ = HM. Ta được AH là đường trung trực của đoạn thẳng MM’ nên AM = AM’ ( tính chất đường trung trực của đoạn thẳng)
Hơn nữa, AM’ < AN ( theo trường hợp 1)
AM < AN
Vậy AM < AN.
b)
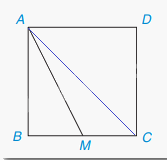
Theo câu a, khi M thay đổi trên BC, M càng xa B thì AM càng lớn. Khi M trùng C thì M xa B nhất nên khi đó AM là lớn nhất.
Chương trình Toán 7 tập 2 Kết nối tri thức tập trung vào các chủ đề quan trọng như biểu thức đại số, phương trình bậc nhất một ẩn, bất đẳng thức và hệ phương trình bậc nhất một ẩn. Trang 63 và 64 của sách giáo khoa tập trung vào việc vận dụng các kiến thức đã học để giải quyết các bài toán thực tế và củng cố lý thuyết.
Bài 1 yêu cầu học sinh giải các phương trình bậc nhất một ẩn. Để giải phương trình, chúng ta cần thực hiện các bước sau:
Ví dụ, để giải phương trình 2x + 3 = 7, ta thực hiện các bước sau:
Bài 2 thường yêu cầu học sinh tìm giá trị của x thỏa mãn một điều kiện nào đó. Để giải bài toán này, chúng ta cần sử dụng các kiến thức về biểu thức đại số và phương trình.
Ví dụ, nếu đề bài yêu cầu tìm x sao cho 3x - 5 = 10, ta giải như sau:
Bài 3 thường là một bài toán ứng dụng, yêu cầu học sinh vận dụng kiến thức đã học để giải quyết một tình huống thực tế. Để giải bài toán này, chúng ta cần:
Bài 4 là một bài tập luyện tập, giúp học sinh củng cố kiến thức và kỹ năng đã học. Các bài tập trong bài 4 có thể tương tự như các bài tập trước đó, hoặc có thể có một số biến đổi nhỏ để tăng độ khó.
Ngoài sách giáo khoa, các em có thể tham khảo thêm các tài liệu sau để học tốt Toán 7:
Hy vọng rằng với lời giải chi tiết và những lời khuyên hữu ích trên đây, các em học sinh sẽ tự tin hơn trong việc giải các bài tập Toán 7 trang 63, 64 SGK Kết nối tri thức. Chúc các em học tập tốt!