Bài 4.32 trang 86 SGK Toán 7 tập 1 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 7. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về các góc tạo bởi một đường thẳng cắt hai đường thẳng song song để giải quyết các vấn đề thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.32 trang 86 SGK Toán 7 tập 1 - Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho tam giác MBC vuông tại M có B= 60°. Gọi A là điểm nằm trên tia đối của tia MB sao cho MA = MB. Chứng minh rằng tam giác ABC là tam giác đều.
Đề bài
Cho tam giác MBC vuông tại M có \(\widehat B\) = 60°. Gọi A là điểm nằm trên tia đối của tia MB sao cho MA = MB. Chứng minh rằng tam giác ABC là tam giác đều.
Phương pháp giải - Xem chi tiết
Chứng minh tam giác ABC cân tại C và có 1 góc bằng 60 độ.
Lời giải chi tiết
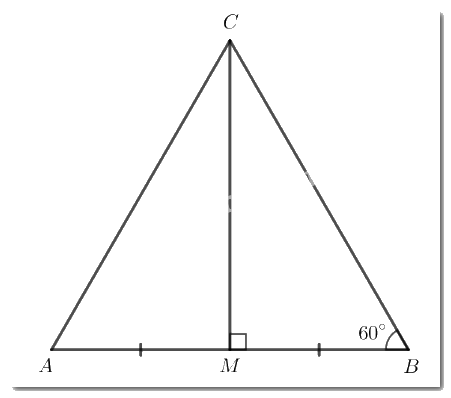
Xét \(\Delta CMB\) và \(\Delta CMA\) có:
MC chung
\(\widehat{BMC}=\widehat{AMC}(=90^0)\)
MB=MA (gt)
=> \(\Delta CMB = \Delta CMA\)(c.g.c)
=> CA = CB (2 cạnh tương ứng).
=> Tam giác ABC cân tại C.
Mà \(\widehat B=\) 60o
=> Tam giác ABC đều.
Bài 4.32 trang 86 SGK Toán 7 tập 1 - Kết nối tri thức là một bài toán ứng dụng thực tế về các góc tạo bởi một đường thẳng cắt hai đường thẳng song song. Để giải bài toán này, học sinh cần nắm vững các kiến thức sau:
Đề bài: (Hình vẽ minh họa)
Cho hình vẽ, biết a // b và góc A1 = 40°. Tính các góc còn lại.
Lời giải:
Kết luận:
Góc B1 = 40°
Góc A2 = 140°
Góc B2 = 140°
Góc B3 = 40°
Góc A3 = 40°
Góc A4 = 140°
Để hiểu rõ hơn về các tính chất của các góc tạo bởi một đường thẳng cắt hai đường thẳng song song, các em có thể làm thêm các bài tập sau:
Lưu ý:
Khi giải các bài tập về góc, các em cần vẽ hình chính xác và ghi nhớ các tính chất của các góc đã học. Ngoài ra, các em cũng nên kiểm tra lại kết quả của mình để đảm bảo tính chính xác.
Kiến thức về các góc tạo bởi một đường thẳng cắt hai đường thẳng song song có ứng dụng rất lớn trong thực tế, ví dụ như trong kiến trúc, xây dựng, hàng hải,...
Ví dụ, trong kiến trúc, các kiến trúc sư sử dụng kiến thức này để thiết kế các tòa nhà có hình dạng đẹp mắt và đảm bảo tính thẩm mỹ. Trong hàng hải, các thủy thủ sử dụng kiến thức này để xác định vị trí của tàu và tránh các chướng ngại vật.
Hy vọng với lời giải chi tiết và dễ hiểu này, các em học sinh sẽ nắm vững kiến thức và tự tin giải các bài tập về góc trong chương trình Toán 7.