Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 7 của giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong SGK Toán 7 tập 1 - Kết nối tri thức, đặc biệt là các bài tập trang 55, 56 và 57.
Mục tiêu của chúng tôi là giúp các em học toán một cách hiệu quả, nắm vững kiến thức và tự tin giải quyết các bài toán khó. Hãy cùng khám phá lời giải chi tiết ngay sau đây!
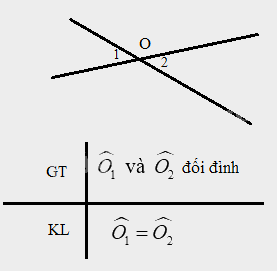
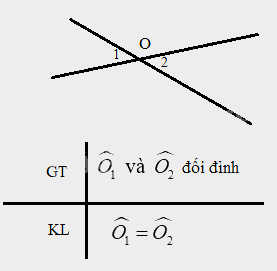
Vẽ hình và viết giả thiết, kết luận của định lí: “ Hai góc đối đỉnh thì bằng nhau”...Em hãy chứng minh định lí: “ Hai góc kề bù bằng nhau thì mỗi góc là một góc vuông”
Vẽ hình và viết giả thiết, kết luận của định lí:
“ Hai góc đối đỉnh thì bằng nhau”
Phương pháp giải:
Vẽ hình
Giả thiết là điều đề bài cho
Kết luận là điều cần chứng minh
Lời giải chi tiết:
Em hãy chứng minh định lí: “ Hai góc kề bù bằng nhau thì mỗi góc là một góc vuông”
Phương pháp giải:
Vẽ hình, viết giả thiết, kết luận rồi chứng minh
Lời giải chi tiết:
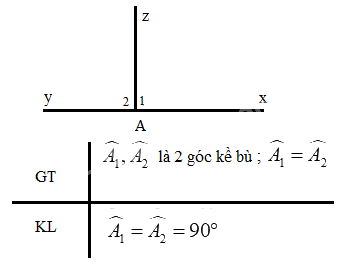
Ta có: \(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \) ( 2 góc kề bù)
Mà \(\widehat {{A_1}} = \widehat {A_2^{}}\)
\(\begin{array}{l} \Rightarrow \widehat {{A_1}} + \widehat {{A_1}} = 180^\circ \\ \Rightarrow 2.\widehat {{A_1}} = 180^\circ \\ \Rightarrow \widehat {{A_1}} = 180^\circ :2 = 90^\circ \end{array}\)
Vậy \(\widehat {{A_1}} = \widehat {A{}_2} = 90^\circ \) (đpcm)

Em có ý kiến gì về hai ý kiến trên?
Phương pháp giải:
Chỉ ra ví dụ chứng tỏ khẳng định không đúng.
Lời giải chi tiết:
Em thấy bạn Vuông nói đúng
Để chứng minh điều này, ta có thể chỉ ra trường hợp 2 góc bằng nhau nhưng không đối đỉnh.
Ví dụ:
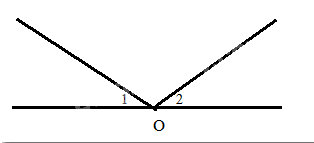
\(\widehat {{O_1}} = \widehat {{O_2}}\) nhưng hai góc này không đối đỉnh
Em hãy chứng minh định lí: “ Hai góc kề bù bằng nhau thì mỗi góc là một góc vuông”
Phương pháp giải:
Vẽ hình, viết giả thiết, kết luận rồi chứng minh
Lời giải chi tiết:
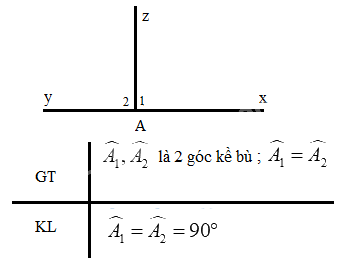
Ta có: \(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \) ( 2 góc kề bù)
Mà \(\widehat {{A_1}} = \widehat {A_2^{}}\)
\(\begin{array}{l} \Rightarrow \widehat {{A_1}} + \widehat {{A_1}} = 180^\circ \\ \Rightarrow 2.\widehat {{A_1}} = 180^\circ \\ \Rightarrow \widehat {{A_1}} = 180^\circ :2 = 90^\circ \end{array}\)
Vậy \(\widehat {{A_1}} = \widehat {A{}_2} = 90^\circ \) (đpcm)
Vẽ hình và viết giả thiết, kết luận của định lí:
“ Hai góc đối đỉnh thì bằng nhau”
Phương pháp giải:
Vẽ hình
Giả thiết là điều đề bài cho
Kết luận là điều cần chứng minh
Lời giải chi tiết:

Em có ý kiến gì về hai ý kiến trên?
Phương pháp giải:
Chỉ ra ví dụ chứng tỏ khẳng định không đúng.
Lời giải chi tiết:
Em thấy bạn Vuông nói đúng
Để chứng minh điều này, ta có thể chỉ ra trường hợp 2 góc bằng nhau nhưng không đối đỉnh.
Ví dụ:
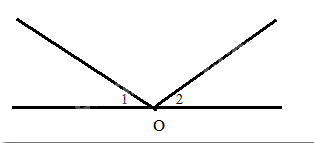
\(\widehat {{O_1}} = \widehat {{O_2}}\) nhưng hai góc này không đối đỉnh
Chương 3 của SGK Toán 7 tập 1 - Kết nối tri thức tập trung vào các kiến thức về biểu thức đại số. Các bài tập trang 55, 56, 57 xoay quanh việc thu gọn biểu thức, tìm giá trị của biểu thức khi biết giá trị của biến, và vận dụng các tính chất của phép cộng, trừ, nhân, chia để đơn giản hóa biểu thức.
Các bài tập trên trang 55 yêu cầu học sinh vận dụng các quy tắc về dấu ngoặc, quy tắc chuyển vế, và các tính chất giao hoán, kết hợp, phân phối để thu gọn biểu thức. Ví dụ:
Để giải các bài tập này, học sinh cần nắm vững các bước sau:
Trang 56 tập trung vào việc tính giá trị của biểu thức đại số khi biết giá trị của các biến. Ví dụ:
Để giải các bài tập này, học sinh cần thực hiện các bước sau:
Trang 57 thường chứa các bài toán ứng dụng thực tế, yêu cầu học sinh vận dụng kiến thức về biểu thức đại số để giải quyết. Ví dụ:
Để giải các bài toán này, học sinh cần:
Khi giải các bài tập về biểu thức đại số, học sinh cần chú ý:
Ngoài SGK Toán 7 tập 1 - Kết nối tri thức, học sinh có thể tham khảo thêm các tài liệu sau:
Hy vọng với những hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải quyết các bài tập trang 55, 56, 57 SGK Toán 7 tập 1 - Kết nối tri thức một cách hiệu quả. Chúc các em học tốt!