Giaitoan.edu.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 1 trang 6, 7 sách giáo khoa Toán 7 tập 1 chương trình Kết nối tri thức. Bài viết này sẽ giúp các em học sinh nắm vững kiến thức, hiểu rõ phương pháp giải bài tập và tự tin hơn trong quá trình học tập môn Toán.
Chúng tôi cung cấp đáp án đầy đủ, kèm theo các bước giải thích chi tiết, giúp các em dễ dàng theo dõi và áp dụng vào các bài tập tương tự.
Tính chỉ số WHtR của ông An và ông Chung....Ta có thể viết ....Giải thích vì sao các số ....Mỗi điểm A,B,C trên trục số Hình 1.4 biểu diễn số hữu tỉ nào?
Tính chỉ số WHtR của ông An và ông Chung
Phương pháp giải:
Tính chỉ số WHtR của mỗi ông:
Chỉ số WHtR = Số đo vòng bụng : Chiều cao
Lời giải chi tiết:
Chỉ số WHtR của ông An là: \(\frac{{108}}{{180}} = 0,6\)
Chỉ số WHtR của ông Chung là: \(\frac{{70}}{{160}} = 0,4375\)
Ta có thể viết \(1,5 = \frac{3}{2} = \frac{6}{4} = \frac{9}{6} = ....\)
Tương tự, em hãy viết ba phân số bằng nhau và bằng:
a) -2,5; b) \(2\frac{3}{4}\)
Phương pháp giải:
a) + Viết số thập phân dưới dạng phân số
+ Nhân cả tử và mẫu với một số nguyên khác 0, ta được phân số mới bằng phân số đã cho.
b) + Viết hỗn số dưới dạng phân số
+ Nhân cả tử và mẫu với một số nguyên khác 0, ta được phân số mới bằng phân số đã cho.
Lời giải chi tiết:
\(\begin{array}{l}a) - 2,5 = \frac{{ - 5}}{2} = \frac{{ - 10}}{4} = \frac{{ - 15}}{6} = ....\\b)2\frac{3}{4} = \frac{{11}}{4} = \frac{{22}}{8} = \frac{{33}}{{12}} = ...\end{array}\)
Giải thích vì sao các số \(8; - 3,3;3\frac{2}{3}\) đều là các số hữu tỉ. Tìm số đối của mỗi số đó
Phương pháp giải:
Số hữu tỉ là số viết được dưới dạng phân số \(\frac{a}{b}(a,b \in Z,b \ne 0)\)
Số đối của số hữu tỉ \(\frac{a}{b}\) là số hữu tỉ \(\frac{{ - a}}{b}\).
Lời giải chi tiết:
Các số \(8; - 3,3;3\frac{2}{3}\) đều là các số hữu tỉ vì các số này đều viết được dưới dạng phân số \(\frac{a}{b}(a,b \in Z,b \ne 0)\)
(\(8 = \frac{8}{1}; - 3,3 = \frac{{ - 33}}{{10}};3\frac{2}{3} = \frac{{11}}{3}\))
Số đối của 8 là -8
Số đối của -3,3 là 3,3
Số đối của \(3\frac{2}{3}\) là \( - 3\frac{2}{3}\)
Tính chỉ số WHtR của ông An và ông Chung
Phương pháp giải:
Tính chỉ số WHtR của mỗi ông:
Chỉ số WHtR = Số đo vòng bụng : Chiều cao
Lời giải chi tiết:
Chỉ số WHtR của ông An là: \(\frac{{108}}{{180}} = 0,6\)
Chỉ số WHtR của ông Chung là: \(\frac{{70}}{{160}} = 0,4375\)
Ta có thể viết \(1,5 = \frac{3}{2} = \frac{6}{4} = \frac{9}{6} = ....\)
Tương tự, em hãy viết ba phân số bằng nhau và bằng:
a) -2,5; b) \(2\frac{3}{4}\)
Phương pháp giải:
a) + Viết số thập phân dưới dạng phân số
+ Nhân cả tử và mẫu với một số nguyên khác 0, ta được phân số mới bằng phân số đã cho.
b) + Viết hỗn số dưới dạng phân số
+ Nhân cả tử và mẫu với một số nguyên khác 0, ta được phân số mới bằng phân số đã cho.
Lời giải chi tiết:
\(\begin{array}{l}a) - 2,5 = \frac{{ - 5}}{2} = \frac{{ - 10}}{4} = \frac{{ - 15}}{6} = ....\\b)2\frac{3}{4} = \frac{{11}}{4} = \frac{{22}}{8} = \frac{{33}}{{12}} = ...\end{array}\)
Giải thích vì sao các số \(8; - 3,3;3\frac{2}{3}\) đều là các số hữu tỉ. Tìm số đối của mỗi số đó
Phương pháp giải:
Số hữu tỉ là số viết được dưới dạng phân số \(\frac{a}{b}(a,b \in Z,b \ne 0)\)
Số đối của số hữu tỉ \(\frac{a}{b}\) là số hữu tỉ \(\frac{{ - a}}{b}\).
Lời giải chi tiết:
Các số \(8; - 3,3;3\frac{2}{3}\) đều là các số hữu tỉ vì các số này đều viết được dưới dạng phân số \(\frac{a}{b}(a,b \in Z,b \ne 0)\)
(\(8 = \frac{8}{1}; - 3,3 = \frac{{ - 33}}{{10}};3\frac{2}{3} = \frac{{11}}{3}\))
Số đối của 8 là -8
Số đối của -3,3 là 3,3
Số đối của \(3\frac{2}{3}\) là \( - 3\frac{2}{3}\)
Mỗi điểm A,B,C trên trục số Hình 1.4 biểu diễn số hữu tỉ nào?

Phương pháp giải:
Xác định số vạch chia và khoảng cách từ gốc O đến điểm đó là bao nhiêu phần.
Các điểm nằm bên trái gốc O biểu diễn số hữu tỉ âm; các điểm nằm bên phải gốc O biểu diễn số hữu tỉ dương.
Lời giải chi tiết:
Đoạn thẳng đơn vị được chia thành 6 phần bằng nhau, lấy một đoạn làm đơn vị mới, đơn vị mới bằng \(\frac{1}{6}\) đơn vị cũ.
Điểm A nằm bên phải gốc O và cách O một đoạn bằng 10 đơn vị mới. Do đó điểm A biểu diễn số hữu tỉ \(\frac{{10}}{6} = \frac{5}{3}\)
Điểm B nằm bên trái gốc O và cách O một đoạn bằng 5 đơn vị mới. Do đó điểm B biểu diễn số hữu tỉ \(\frac{{ - 5}}{6}\)
Điểm C nằm bên trái gốc O và cách O một đoạn bằng 13 đơn vị mới. Do đó điểm C biểu diễn số hữu tỉ \(\frac{{ - 13}}{6}\)
Biểu diễn các số hữu tỉ \(\frac{5}{4}\) và \(\frac{{ - 5}}{4}\)trên trục số.
Phương pháp giải:
Chia đoạn thẳng đơn vị thành 4 phần bằng nhau. Lấy một đoạn làm đơn vị mới ( đơn vị mới bằng \(\frac{1}{4}\) đơn vị cũ)
Số hữu tỉ \(\frac{5}{4}\) được biểu diễn bằng điểm nằm bên phải gốc O, cách gốc O một đoạn bằng 5 đơn vị mới.
Số hữu tỉ \(\frac{{ - 5}}{4}\) được biểu diễn bằng điểm nằm bên trái gốc O, cách gốc O một đoạn bằng 5 đơn vị mới.
Lời giải chi tiết:
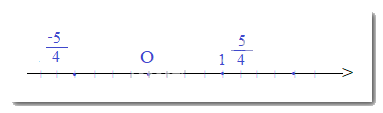
Biểu diễn các số hữu tỉ \(\frac{5}{4}\) và \(\frac{{ - 5}}{4}\)trên trục số.
Phương pháp giải:
Chia đoạn thẳng đơn vị thành 4 phần bằng nhau. Lấy một đoạn làm đơn vị mới ( đơn vị mới bằng \(\frac{1}{4}\) đơn vị cũ)
Số hữu tỉ \(\frac{5}{4}\) được biểu diễn bằng điểm nằm bên phải gốc O, cách gốc O một đoạn bằng 5 đơn vị mới.
Số hữu tỉ \(\frac{{ - 5}}{4}\) được biểu diễn bằng điểm nằm bên trái gốc O, cách gốc O một đoạn bằng 5 đơn vị mới.
Lời giải chi tiết:

Mỗi điểm A,B,C trên trục số Hình 1.4 biểu diễn số hữu tỉ nào?

Phương pháp giải:
Xác định số vạch chia và khoảng cách từ gốc O đến điểm đó là bao nhiêu phần.
Các điểm nằm bên trái gốc O biểu diễn số hữu tỉ âm; các điểm nằm bên phải gốc O biểu diễn số hữu tỉ dương.
Lời giải chi tiết:
Đoạn thẳng đơn vị được chia thành 6 phần bằng nhau, lấy một đoạn làm đơn vị mới, đơn vị mới bằng \(\frac{1}{6}\) đơn vị cũ.
Điểm A nằm bên phải gốc O và cách O một đoạn bằng 10 đơn vị mới. Do đó điểm A biểu diễn số hữu tỉ \(\frac{{10}}{6} = \frac{5}{3}\)
Điểm B nằm bên trái gốc O và cách O một đoạn bằng 5 đơn vị mới. Do đó điểm B biểu diễn số hữu tỉ \(\frac{{ - 5}}{6}\)
Điểm C nằm bên trái gốc O và cách O một đoạn bằng 13 đơn vị mới. Do đó điểm C biểu diễn số hữu tỉ \(\frac{{ - 13}}{6}\)
Mục 1 trang 6, 7 SGK Toán 7 tập 1 - Kết nối tri thức giới thiệu về tập hợp các số tự nhiên, số nguyên, số hữu tỉ và các phép toán cơ bản trên chúng. Đây là nền tảng quan trọng để học các kiến thức toán học nâng cao hơn. Việc nắm vững các khái niệm và quy tắc trong mục này là rất cần thiết để giải quyết các bài toán trong chương trình học.
Mục 1 trang 6, 7 SGK Toán 7 tập 1 - Kết nối tri thức bao gồm các bài tập rèn luyện về:
Bài 1: Viết các số sau dưới dạng phân số: -3; 0,5; 1,25.
Giải:
Bài 2: Điền vào chỗ trống: ... > ... > ... > ... > ...
Giải: (Bài giải cụ thể sẽ được điền vào đây, tùy thuộc vào nội dung bài tập)
Bài 3: Thực hiện các phép tính sau: a) 1/2 + 1/3; b) 2/5 - 1/4; c) 3/7 * 2/5; d) 4/9 : 1/3.
Giải:
Ngoài SGK Toán 7 tập 1 - Kết nối tri thức, các em có thể tham khảo thêm các tài liệu sau:
Hy vọng bài viết này đã cung cấp cho các em những kiến thức và kỹ năng cần thiết để giải quyết các bài tập trong mục 1 trang 6, 7 SGK Toán 7 tập 1 - Kết nối tri thức. Chúc các em học tập tốt!