Bài 9.25 trang 76 SGK Toán 7 tập 2 thuộc chương trình Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về ứng dụng tỉ lệ thức vào các bài toán thực tế. Bài tập này thường yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các vấn đề liên quan đến việc chia tỉ lệ.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9.25 trang 76 SGK Toán 7 tập 2, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
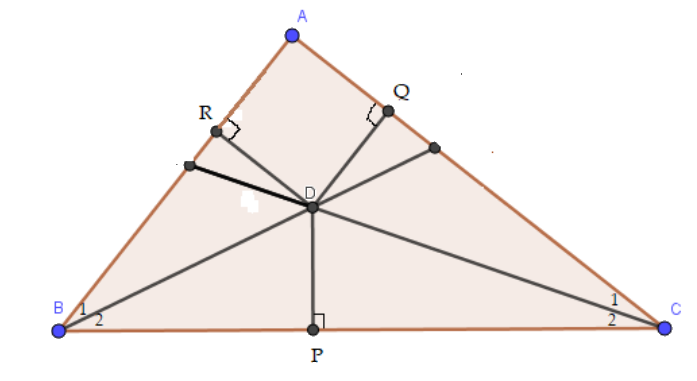
Trong tam giác ABC, hai đường phân giác của các góc B và C cắt nhau tại D. Kẻ DP vuông góc với BC, DQ vuông góc với CA, DR vuông góc với AB. a) Hãy giải thích tại sao DP = DR. b) Hãy giải thích tại sao DP = DQ. c) Từ câu a và b suy ra DR = DQ. Tại sao D nằm trên tia phân giác của góc A? ( Đây là một cách chứng minh định lí 2)
Đề bài
Trong tam giác ABC, hai đường phân giác của các góc B và C cắt nhau tại D. Kẻ DP vuông góc với BC, DQ vuông góc với CA, DR vuông góc với AB.
a) Hãy giải thích tại sao DP = DR.
b) Hãy giải thích tại sao DP = DQ.
c) Từ câu a và b suy ra DR = DQ. Tại sao D nằm trên tia phân giác của góc A? ( Đây là một cách chứng minh định lí 2)
Phương pháp giải - Xem chi tiết
Sử dụng tính chất tia phân giác của một góc, xét 2 tam giác bằng nhau, suy ra các cạnh tương ứng bằng nhau.
Lời giải chi tiết
a) Vì BD là tia phân giác của góc ABC nên \(\widehat {{B_1}} = \widehat {{B_2}} = \dfrac{1}{2}.\widehat {ABC}\)
Vì CD là tia phân giác của góc ACB nên \(\widehat {{C_1}} = \widehat {{C_2}} = \dfrac{1}{2}.\widehat {ACB}\)
Xét \(\Delta BDP\) vuông tại P và \(\Delta BDR\) vuông tại R, ta có:
\(\widehat {{B_2}} = \widehat {{B_1}}\)
BD chung
nên \(\Delta BDP = \Delta BDR\) (cạnh huyền – góc nhọn)
suy ra DP = DR (2 cạnh tương ứng) (1)
b) Xét \(\Delta CDP\) vuông tại P và \(\Delta CDQ\) vuông tại Q, ta có:
\(\widehat {{C_2}} = \widehat {{C_1}}\)
CD chung
nên \(\Delta CDP = \Delta CDQ\) (cạnh huyền – góc nhọn)
suy ra DP = DQ ( 2 cạnh tương ứng) (2)
c) Từ (1) và (2), ta được: DR = DQ (cùng bằng DP).
D nằm trên tia phân giác của góc A do D cách đều AB và AC.
Bài 9.25 SGK Toán 7 tập 2 Kết nối tri thức yêu cầu chúng ta giải quyết một bài toán thực tế liên quan đến việc chia tỉ lệ. Để giải bài này, chúng ta cần nắm vững các khái niệm về tỉ lệ thức, tính chất của tỉ lệ thức và cách áp dụng chúng vào việc giải toán.
Một đội công nhân cần sửa một đoạn đường dài 120m. Để hoàn thành công việc trong 3 ngày, mỗi ngày đội công nhân đó cần sửa bao nhiêu mét đường?
Bài toán này yêu cầu chúng ta tìm số mét đường mà đội công nhân cần sửa mỗi ngày để hoàn thành công việc trong 3 ngày. Chúng ta có thể sử dụng tỉ lệ thức để giải bài toán này. Tổng chiều dài đoạn đường (120m) tỉ lệ thuận với số ngày làm việc (3 ngày). Số mét đường sửa mỗi ngày là đại lượng cần tìm.
Gọi x là số mét đường mà đội công nhân cần sửa mỗi ngày.
Ta có tỉ lệ thức:
x / 120 = 1 / 3
Giải tỉ lệ thức, ta được:
x = 120 * (1/3)
x = 40
Vậy, mỗi ngày đội công nhân đó cần sửa 40 mét đường.
Để hoàn thành công việc sửa đoạn đường dài 120m trong 3 ngày, đội công nhân cần sửa 40 mét đường mỗi ngày.
Bài toán này có thể được mở rộng bằng cách thay đổi tổng chiều dài đoạn đường, số ngày làm việc hoặc số lượng công nhân. Việc thay đổi các yếu tố này sẽ ảnh hưởng đến số mét đường mà mỗi công nhân cần sửa mỗi ngày.
Nếu đoạn đường dài 150m và đội công nhân cần hoàn thành công việc trong 5 ngày, thì mỗi ngày đội công nhân đó cần sửa bao nhiêu mét đường?
Lời giải:
Gọi y là số mét đường mà đội công nhân cần sửa mỗi ngày.
Ta có tỉ lệ thức:
y / 150 = 1 / 5
Giải tỉ lệ thức, ta được:
y = 150 * (1/5)
y = 30
Vậy, mỗi ngày đội công nhân đó cần sửa 30 mét đường.
Hy vọng với lời giải chi tiết và hướng dẫn trên, các em học sinh sẽ hiểu rõ hơn về cách giải bài 9.25 trang 76 SGK Toán 7 tập 2 - Kết nối tri thức. Chúc các em học tập tốt!