Bài 4.14 trang 73 SGK Toán 7 tập 1 thuộc chương 4: Biểu đồ hình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về góc và các tính chất liên quan để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.14 trang 73 SGK Toán 7 tập 1 - Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chứng minh rằng hai tam giác ADE và BCE trong Hình 4.41 bằng nhau.
Đề bài
Chứng minh rằng hai tam giác ADE và BCE trong Hình 4.41 bằng nhau.
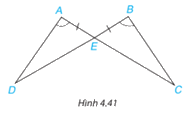
Phương pháp giải - Xem chi tiết
Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.
Lời giải chi tiết
Xét hai tam giác ADE và BCE có:
\(\widehat A = \widehat B\)
AE=BE
\(\widehat {AED} = \widehat {BEC}\)(đối đỉnh)
Vậy \(\Delta ADE = \Delta BCE\)(g.c.g)
Bài 4.14 trang 73 SGK Toán 7 tập 1 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 7. Bài tập này giúp học sinh củng cố kiến thức về góc, các loại góc (góc nhọn, góc vuông, góc tù, góc bẹt) và các tính chất liên quan đến góc. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản và áp dụng các phương pháp giải toán phù hợp.
Bài tập 4.14 yêu cầu học sinh quan sát hình vẽ và thực hiện các yêu cầu sau:
Để giải bài tập này, học sinh có thể áp dụng các phương pháp sau:
(Ở đây sẽ là lời giải chi tiết của bài tập 4.14, bao gồm các bước giải, hình vẽ minh họa và giải thích rõ ràng. Ví dụ:)
Lời giải:
a) Các góc có trên hình là: ∠ABC, ∠BCD, ∠CDE, ∠DEA, ∠EAB.
b) Phân loại các góc:
c) Giả sử ∠ABC = 30°, ∠CDE = 120°. (Các giá trị này cần dựa trên hình vẽ cụ thể trong SGK)
d) So sánh:
Để củng cố kiến thức về góc và các tính chất liên quan, học sinh có thể làm thêm các bài tập tương tự trong SGK và sách bài tập Toán 7 tập 1 - Kết nối tri thức. Ngoài ra, học sinh có thể tìm hiểu thêm về các loại góc đặc biệt như góc kề bù, góc đối đỉnh và các ứng dụng của góc trong thực tế.
Bài 4.14 trang 73 SGK Toán 7 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về góc và các tính chất liên quan. Bằng cách áp dụng các phương pháp giải toán phù hợp và thực hành thường xuyên, học sinh có thể giải quyết bài tập này một cách hiệu quả và đạt kết quả tốt trong môn Toán.
| Loại góc | Số đo |
|---|---|
| Góc nhọn | < 90° |
| Góc vuông | = 90° |
| Góc tù | > 90° và < 180° |
| Góc bẹt | = 180° |