Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài tập mục 2 trang 32, 33 SGK Toán 7 tập 2 - Kết nối tri thức. Bài viết này sẽ giúp học sinh hiểu rõ phương pháp giải và tự tin làm bài tập về nhà.
Chúng tôi cung cấp đáp án chính xác, dễ hiểu, kèm theo các bước giải chi tiết, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Cho hai đa thức P = x^4 + 3x^3 – 5x^2 + 7x và Q = -x^3 + 4x^2 – 2x +1 Tìm hiệu P – Q bằng cách bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc và thu gọn.
Cho hai đa thức P = x4 + 3x3 – 5x2 + 7x và Q = -x3 + 4x2 – 2x +1
Tìm hiệu P – Q bằng cách bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc và thu gọn.
Phương pháp giải:
+ Bước 1: Bỏ dấu ngoặc: Trước dấu ngoặc là dấu “ –“ thì ta bỏ dấu ngoặc đồng thời đổi dấu tất cả các số hạng trong ngoặc.
+Bước 2: Nhóm các hạng tử cùng bậc
+ Bước 3: Thu gọn
Lời giải chi tiết:
Ta có: P – Q = x4 + 3x3 – 5x2 + 7x – (-x3 + 4x2 – 2x +1)
= x4 + 3x3 – 5x2 + 7x + x3 - 4x2 + 2x – 1
= x4 + (3x3+ x3 ) + (– 5x2 - 4x2 ) + (7x + 2x ) – 1
= x4 + 4x3 – 9x2 + 9x – 1
Cho đa thức A = x4 – 3x2 – 2x + 1. Tìm các đa thức B và C sao cho:
A + B = 2x5 + 5x3 – 2
A – C = x3
Phương pháp giải:
B = (A + B) – A
C = A – (A – C)
Thực hiện phép trừ đa thức:
Bỏ dấu ngoặc: Trước dấu ngoặc là dấu “ –“ thì ta bỏ dấu ngoặc đồng thời đổi dấu tất cả các số hạng trong ngoặc rồi nhóm các hạng tử cùng bậc
Lời giải chi tiết:
Ta có:
B = (A + B) – A = 2x5 + 5x3 – 2 – (x4 – 3x2 – 2x + 1)
= 2x5 + 5x3 – 2 – x4 + 3x2 + 2x - 1
= 2x5 – x4 + 5x3 + 3x2 + 2x + (-2 – 1)
= 2x5 – x4 + 5x3 + 3x2 + 2x – 3
C = A – (A – C) = x4 – 3x2 – 2x + 1 – x3
= x4 – x3– 3x2 – 2x + 1
Vậy B = 2x5 – x4 + 5x3 + 3x2 + 2x – 3
C = x4 – x3– 3x2 – 2x + 1
Cho hai đa thức P = x4 + 3x3 – 5x2 + 7x và Q = -x3 + 4x2 – 2x +1
Tìm hiệu P – Q bằng cách đặt tính trừ: đặt đa thức Q dưới đa thức P sao cho các hạng tử cùng bậc thẳng cột với nhau rồi trừ theo từng cột.
Phương pháp giải:
Bước 1: Đặt đa thức Q dưới đa thức P sao cho các hạng tử cùng bậc thẳng cột với nhau
Bước 2: Trừ theo từng cột
Lời giải chi tiết:
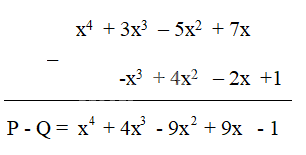
2. Trừ hai đa thức một biến
Cho hai đa thức P = x4 + 3x3 – 5x2 + 7x và Q = -x3 + 4x2 – 2x +1
Tìm hiệu P – Q bằng cách bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc và thu gọn.
Phương pháp giải:
+ Bước 1: Bỏ dấu ngoặc: Trước dấu ngoặc là dấu “ –“ thì ta bỏ dấu ngoặc đồng thời đổi dấu tất cả các số hạng trong ngoặc.
+Bước 2: Nhóm các hạng tử cùng bậc
+ Bước 3: Thu gọn
Lời giải chi tiết:
Ta có: P – Q = x4 + 3x3 – 5x2 + 7x – (-x3 + 4x2 – 2x +1)
= x4 + 3x3 – 5x2 + 7x + x3 - 4x2 + 2x – 1
= x4 + (3x3+ x3 ) + (– 5x2 - 4x2 ) + (7x + 2x ) – 1
= x4 + 4x3 – 9x2 + 9x – 1
Cho hai đa thức P = x4 + 3x3 – 5x2 + 7x và Q = -x3 + 4x2 – 2x +1
Tìm hiệu P – Q bằng cách đặt tính trừ: đặt đa thức Q dưới đa thức P sao cho các hạng tử cùng bậc thẳng cột với nhau rồi trừ theo từng cột.
Phương pháp giải:
Bước 1: Đặt đa thức Q dưới đa thức P sao cho các hạng tử cùng bậc thẳng cột với nhau
Bước 2: Trừ theo từng cột
Lời giải chi tiết:
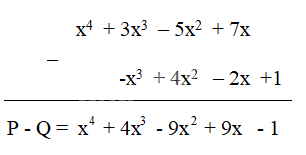
Cho hai đa thức:
M = 0,5x4 – 4x3 + 2x – 2,5 và N = 2x3 + x2 + 1,5
Hãy tính hiệu M - N ( trình bày theo 2 cách)
Phương pháp giải:
Cách 1: Bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc.
Cách 2: Đặt tính trừ sao cho các hạng tử cùng bậc đặt thẳng cột với nhau rồi trừ theo từng cột.
Lời giải chi tiết:
Cách 1:
M - N = (0,5x4 – 4x3 + 2x – 2,5) - ( 2x3 + x2 + 1,5)
= 0,5x4 – 4x3 + 2x – 2,5 - 2x3 - x2 - 1,5
= 0,5x4 + (– 4x3 - 2x3 ) - x2 + 2x + (-2,5 - 1,5)
= 0,5x4 + (– 6x3 ) - x2 + 2x + (-4)
= 0,5x4 – 6x3 - x2 + 2x – 4
Cách 2:
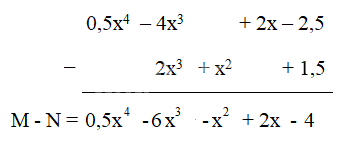
Cho đa thức A = x4 – 3x2 – 2x + 1. Tìm các đa thức B và C sao cho:
A + B = 2x5 + 5x3 – 2
A – C = x3
Phương pháp giải:
B = (A + B) – A
C = A – (A – C)
Thực hiện phép trừ đa thức:
Bỏ dấu ngoặc: Trước dấu ngoặc là dấu “ –“ thì ta bỏ dấu ngoặc đồng thời đổi dấu tất cả các số hạng trong ngoặc rồi nhóm các hạng tử cùng bậc
Lời giải chi tiết:
Ta có:
B = (A + B) – A = 2x5 + 5x3 – 2 – (x4 – 3x2 – 2x + 1)
= 2x5 + 5x3 – 2 – x4 + 3x2 + 2x - 1
= 2x5 – x4 + 5x3 + 3x2 + 2x + (-2 – 1)
= 2x5 – x4 + 5x3 + 3x2 + 2x – 3
C = A – (A – C) = x4 – 3x2 – 2x + 1 – x3
= x4 – x3– 3x2 – 2x + 1
Vậy B = 2x5 – x4 + 5x3 + 3x2 + 2x – 3
C = x4 – x3– 3x2 – 2x + 1
Cho hai đa thức:
M = 0,5x4 – 4x3 + 2x – 2,5 và N = 2x3 + x2 + 1,5
Hãy tính hiệu M - N ( trình bày theo 2 cách)
Phương pháp giải:
Cách 1: Bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc.
Cách 2: Đặt tính trừ sao cho các hạng tử cùng bậc đặt thẳng cột với nhau rồi trừ theo từng cột.
Lời giải chi tiết:
Cách 1:
M - N = (0,5x4 – 4x3 + 2x – 2,5) - ( 2x3 + x2 + 1,5)
= 0,5x4 – 4x3 + 2x – 2,5 - 2x3 - x2 - 1,5
= 0,5x4 + (– 4x3 - 2x3 ) - x2 + 2x + (-2,5 - 1,5)
= 0,5x4 + (– 6x3 ) - x2 + 2x + (-4)
= 0,5x4 – 6x3 - x2 + 2x – 4
Cách 2:
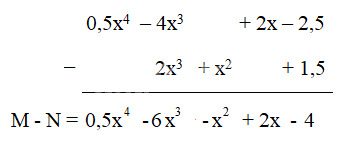
Mục 2 của chương trình Toán 7 tập 2 - Kết nối tri thức tập trung vào việc ôn tập và củng cố các kiến thức về biểu thức đại số, các phép toán trên đa thức, và ứng dụng của chúng trong giải toán. Việc nắm vững kiến thức này là nền tảng quan trọng cho việc học tập các chương trình Toán học ở các lớp trên.
Bài tập mục 2 trang 32, 33 SGK Toán 7 tập 2 - Kết nối tri thức bao gồm các dạng bài tập khác nhau, yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các vấn đề cụ thể. Các dạng bài tập thường gặp bao gồm:
Để thu gọn biểu thức, ta cần thực hiện các phép toán cộng, trừ, nhân, chia các đơn thức đồng dạng. Ví dụ, để thu gọn biểu thức 3x + 2x - 5x, ta thực hiện như sau:
3x + 2x - 5x = (3 + 2 - 5)x = 0x = 0
Để tính giá trị của biểu thức, ta thay các giá trị cụ thể của biến vào biểu thức và thực hiện các phép toán. Ví dụ, để tính giá trị của biểu thức 2x + 3y khi x = 1 và y = 2, ta thực hiện như sau:
2x + 3y = 2(1) + 3(2) = 2 + 6 = 8
Để chứng minh đẳng thức, ta cần biến đổi một trong hai vế của đẳng thức để nó trở thành vế còn lại. Ví dụ, để chứng minh đẳng thức (a + b)2 = a2 + 2ab + b2, ta thực hiện như sau:
(a + b)2 = (a + b)(a + b) = a(a + b) + b(a + b) = a2 + ab + ba + b2 = a2 + 2ab + b2
Để học tập môn Toán 7 hiệu quả, các em học sinh cần:
Việc giải bài tập mục 2 trang 32, 33 SGK Toán 7 tập 2 - Kết nối tri thức là một bước quan trọng trong quá trình học tập môn Toán 7. Hy vọng rằng, với những hướng dẫn chi tiết và các mẹo học tập hiệu quả mà chúng tôi đã cung cấp, các em học sinh sẽ tự tin hơn trong việc giải quyết các bài tập và đạt kết quả tốt trong môn học này.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục tri thức. Chúc các em học tập tốt!