Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 7 tập 2 Kết nối tri thức. Bài viết này sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 77, 78, 79 của sách giáo khoa.
Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức. Vì vậy, giaitoan.edu.vn luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất cho các em.
Vẽ tam giác ABC ( không tù) và ba đường trung trực của các đoạn BC, CA, AB. Quan sát hình và cho biết ba đường trung trực đó có cùng đi qua một điểm hay không?
Mỗi tam giác có mấy đường trung trực
Phương pháp giải:
Đường trung trực của đoạn thẳng là đường vuông góc với đoạn thẳng tại trung điểm của đoạn thẳng đó.
Lời giải chi tiết:
Mỗi tam giác có 3 đường trung trực.
Em hãy trả lời câu hỏi trong tình huống mở đầu.
Phương pháp giải:
Địa điểm khoan giếng cách đều 3 ngôi nhà
Lời giải chi tiết:
3 ngôi nhà không thẳng hàng nên tạo thành 1 tam giác, ta gọi là tam giác ABC.
Điểm khoan giếng cách đều 3 ngôi nhà khi và chỉ khi điểm khoan giếng là giao điểm của 3 đường trung trực của tam giác ABC.
Vậy, ta cần vẽ 2 đường trung trực của tam giác ABC, chúng cắt nhau tại đâu thì đó là điểm cần khoan giếng.
Vẽ tam giác ABC ( không tù) và ba đường trung trực của các đoạn BC, CA, AB. Quan sát hình và cho biết ba đường trung trực đó có cùng đi qua một điểm hay không?
Phương pháp giải:
Đường trung trực của đoạn thẳng là đường vuông góc với đoạn thẳng tại trung điểm của đoạn thẳng đó.
Lời giải chi tiết:

Ba đường trung trực DP, DQ, DR cùng cắt nhau tại điểm D.
Dùng tính chất đường trung trực của một đoạn thẳng, hãy lập luận để suy ra tính chất nói ở HĐ1 bằng cách trả lời các câu hỏi sau:
Cho O là giao điểm các đường trung trực của hai cạnh BC và CA (H.9.38)
a) Tại sao OB = OC, OC = OA.
b) Điểm O có nằm trên đường trung trực của AB không?
Phương pháp giải:
Gọi M là trung điểm BC, N là trung điểm AC
a) Chứng minh \(\Delta OBM = \Delta OCM\)(c – g – c), \(\Delta OAN = \Delta OCN\)(c – g – c)
b) Điểm cách đều hai đầu mút của đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đấy.
Lời giải chi tiết:
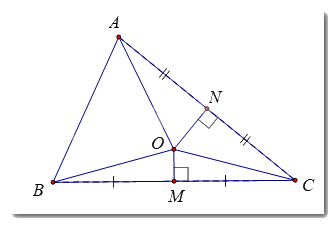
a)
Gọi M là trung điểm của BC, N là trung điểm AC.
Xét \(\Delta OBM\) và \(\Delta OCM\) có:
BM = CM (gt)
\(\widehat {OMB} = \widehat {OMC} = {90^0}\)
OM chung
\( \Rightarrow \Delta OBM = \Delta OCM\left( {c - g - c} \right)\)
\( \Rightarrow OB = OC\)(cạnh tương ứng)
Chứng minh tương tự: \(\Delta OAN = \Delta OCN\) (c – g – c) \( \Rightarrow OA = OC\) (cạnh tương ứng)
b) Ta có: \(\left\{ \begin{array}{l}OA = OC\\OB = OC\end{array} \right.\left( {cmt} \right) \Rightarrow OA = OB\)
\( \Rightarrow O\) cách đều hai đầu mút của đoạn thẳng AB
\( \Rightarrow O\) nằm trên đường trung trực của đoạn thẳng AB (tính chất đường trung trực của đoạn thẳng)
Chứng minh rằng trong tam giác đều ABC, trọng tâm G cách đều 3 đỉnh của tam giác đó.
Phương pháp giải:
Áp dụng: Trong tam giác cân ABC cân tại A, đường trung tuyến BN cũng là đường trung trực của AC
Từ đó chứng minh G là giao điểm ba đường trung trực của tam giác ABC
Lời giải chi tiết:
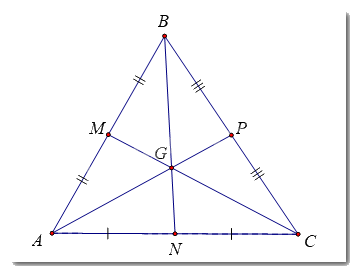
Tam giác ABC đều nên AB = BC = CA
Tam giác ABC cân tại B có BN là đường trung tuyến
\( \Rightarrow BN\)là đường trung trực của đoạn thẳng AC
Tam giác BAC cân tại A có AP là đường trung tuyến
\( \Rightarrow AP\)là đường trung trực của đoạn thẳng BC
Mà \(BN \cap AP = G\)
\( \Rightarrow G\)là giao điểm ba đường trung trực của tam giác ABC
\( \Rightarrow GA = GB = GC\).
Sử dụng tính chất đường trung trực của một đoạn thẳng, hãy giải thích nếu điểm Q cách đều 3 đỉnh của tam giác ABC thì Q phải là giao điểm ba đường trung trực của tam giác ABC.
Phương pháp giải:
Điểm cách đều 2 mút của đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng.
Lời giải chi tiết:
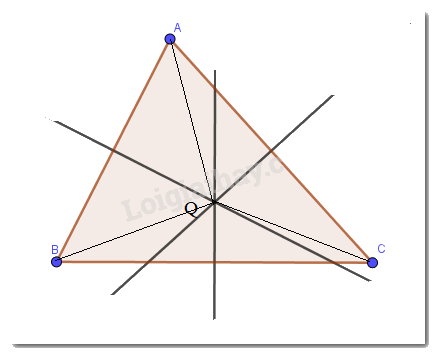
Vì Q cách đều 3 đỉnh của tam giác ABC nên QA=QB=QC
Vì QA=QB nên Q nằm trên đường trung trực của đoạn thẳng AB (tính chất đường trung trực của đoạn thẳng).
Vì QA=QC nên Q nằm trên đường trung trực của đoạn thẳng AC (tính chất đường trung trực của đoạn thẳng).
Vì QB=QC nên Q nằm trên đường trung trực của đoạn thẳng BC (tính chất đường trung trực của đoạn thẳng).
Vậy Q là giao điểm của 3 đường trung trực của tam giác ABC.
Mỗi tam giác có mấy đường trung trực
Phương pháp giải:
Đường trung trực của đoạn thẳng là đường vuông góc với đoạn thẳng tại trung điểm của đoạn thẳng đó.
Lời giải chi tiết:
Mỗi tam giác có 3 đường trung trực.
Vẽ tam giác ABC ( không tù) và ba đường trung trực của các đoạn BC, CA, AB. Quan sát hình và cho biết ba đường trung trực đó có cùng đi qua một điểm hay không?
Phương pháp giải:
Đường trung trực của đoạn thẳng là đường vuông góc với đoạn thẳng tại trung điểm của đoạn thẳng đó.
Lời giải chi tiết:
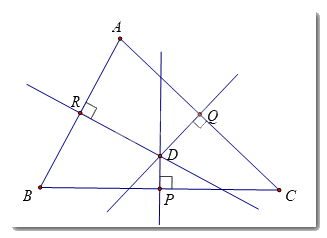
Ba đường trung trực DP, DQ, DR cùng cắt nhau tại điểm D.
Dùng tính chất đường trung trực của một đoạn thẳng, hãy lập luận để suy ra tính chất nói ở HĐ1 bằng cách trả lời các câu hỏi sau:
Cho O là giao điểm các đường trung trực của hai cạnh BC và CA (H.9.38)
a) Tại sao OB = OC, OC = OA.
b) Điểm O có nằm trên đường trung trực của AB không?
Phương pháp giải:
Gọi M là trung điểm BC, N là trung điểm AC
a) Chứng minh \(\Delta OBM = \Delta OCM\)(c – g – c), \(\Delta OAN = \Delta OCN\)(c – g – c)
b) Điểm cách đều hai đầu mút của đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đấy.
Lời giải chi tiết:
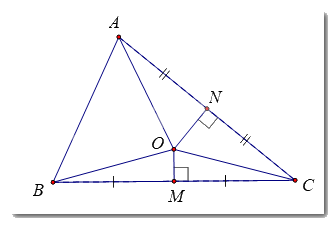
a)
Gọi M là trung điểm của BC, N là trung điểm AC.
Xét \(\Delta OBM\) và \(\Delta OCM\) có:
BM = CM (gt)
\(\widehat {OMB} = \widehat {OMC} = {90^0}\)
OM chung
\( \Rightarrow \Delta OBM = \Delta OCM\left( {c - g - c} \right)\)
\( \Rightarrow OB = OC\)(cạnh tương ứng)
Chứng minh tương tự: \(\Delta OAN = \Delta OCN\) (c – g – c) \( \Rightarrow OA = OC\) (cạnh tương ứng)
b) Ta có: \(\left\{ \begin{array}{l}OA = OC\\OB = OC\end{array} \right.\left( {cmt} \right) \Rightarrow OA = OB\)
\( \Rightarrow O\) cách đều hai đầu mút của đoạn thẳng AB
\( \Rightarrow O\) nằm trên đường trung trực của đoạn thẳng AB (tính chất đường trung trực của đoạn thẳng)
Chứng minh rằng trong tam giác đều ABC, trọng tâm G cách đều 3 đỉnh của tam giác đó.
Phương pháp giải:
Áp dụng: Trong tam giác cân ABC cân tại A, đường trung tuyến BN cũng là đường trung trực của AC
Từ đó chứng minh G là giao điểm ba đường trung trực của tam giác ABC
Lời giải chi tiết:
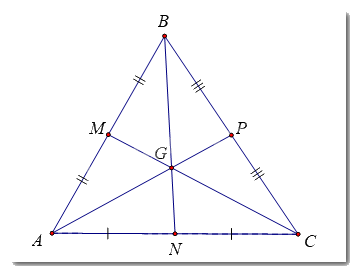
Tam giác ABC đều nên AB = BC = CA
Tam giác ABC cân tại B có BN là đường trung tuyến
\( \Rightarrow BN\)là đường trung trực của đoạn thẳng AC
Tam giác BAC cân tại A có AP là đường trung tuyến
\( \Rightarrow AP\)là đường trung trực của đoạn thẳng BC
Mà \(BN \cap AP = G\)
\( \Rightarrow G\)là giao điểm ba đường trung trực của tam giác ABC
\( \Rightarrow GA = GB = GC\).
Em hãy trả lời câu hỏi trong tình huống mở đầu.
Phương pháp giải:
Địa điểm khoan giếng cách đều 3 ngôi nhà
Lời giải chi tiết:
3 ngôi nhà không thẳng hàng nên tạo thành 1 tam giác, ta gọi là tam giác ABC.
Điểm khoan giếng cách đều 3 ngôi nhà khi và chỉ khi điểm khoan giếng là giao điểm của 3 đường trung trực của tam giác ABC.
Vậy, ta cần vẽ 2 đường trung trực của tam giác ABC, chúng cắt nhau tại đâu thì đó là điểm cần khoan giếng.
Sử dụng tính chất đường trung trực của một đoạn thẳng, hãy giải thích nếu điểm Q cách đều 3 đỉnh của tam giác ABC thì Q phải là giao điểm ba đường trung trực của tam giác ABC.
Phương pháp giải:
Điểm cách đều 2 mút của đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng.
Lời giải chi tiết:
Vì Q cách đều 3 đỉnh của tam giác ABC nên QA=QB=QC
Vì QA=QB nên Q nằm trên đường trung trực của đoạn thẳng AB (tính chất đường trung trực của đoạn thẳng).
Vì QA=QC nên Q nằm trên đường trung trực của đoạn thẳng AC (tính chất đường trung trực của đoạn thẳng).
Vì QB=QC nên Q nằm trên đường trung trực của đoạn thẳng BC (tính chất đường trung trực của đoạn thẳng).
Vậy Q là giao điểm của 3 đường trung trực của tam giác ABC.
Mục 1 của chương trình Toán 7 tập 2 Kết nối tri thức tập trung vào việc ôn tập và củng cố các kiến thức về số hữu tỉ, phép cộng, trừ, nhân, chia số hữu tỉ. Các bài tập trong mục này giúp học sinh rèn luyện kỹ năng tính toán, so sánh và sắp xếp các số hữu tỉ, đồng thời áp dụng các kiến thức đã học vào giải quyết các bài toán thực tế.
Bài 1 yêu cầu học sinh nhắc lại các kiến thức cơ bản về số hữu tỉ, bao gồm định nghĩa, cách biểu diễn, so sánh và sắp xếp các số hữu tỉ. Bài tập này giúp học sinh hệ thống lại kiến thức đã học và chuẩn bị cho các bài tập tiếp theo.
Bài 2 tập trung vào việc rèn luyện kỹ năng thực hiện các phép tính cộng, trừ, nhân, chia số hữu tỉ. Các bài tập trong bài này có độ khó tăng dần, từ các phép tính đơn giản đến các phép tính phức tạp hơn. Học sinh cần nắm vững các quy tắc thực hiện các phép tính này để giải quyết các bài tập một cách chính xác.
Bài 3 là một bài tập vận dụng, yêu cầu học sinh áp dụng các kiến thức đã học để giải quyết các bài toán thực tế. Bài tập này giúp học sinh rèn luyện kỹ năng tư duy và giải quyết vấn đề, đồng thời củng cố kiến thức đã học.
Dưới đây là hướng dẫn giải chi tiết cho từng bài tập trong mục 1 trang 77, 78, 79 SGK Toán 7 tập 2 Kết nối tri thức:
Bài 1.1: (Nêu yêu cầu bài tập và giải thích chi tiết cách giải). Ví dụ: Bài 1.1 yêu cầu học sinh điền vào chỗ trống để hoàn thành các câu sau: a) Số hữu tỉ là số ...; b) Hai số hữu tỉ được gọi là đối nhau nếu ... Giải thích: a) Số hữu tỉ là số có thể được viết dưới dạng phân số a/b, với a là số nguyên và b là số nguyên dương. b) Hai số hữu tỉ được gọi là đối nhau nếu tổng của chúng bằng 0.
Bài 1.2: (Nêu yêu cầu bài tập và giải thích chi tiết cách giải).
...
Bài 2.1: (Nêu yêu cầu bài tập và giải thích chi tiết cách giải). Ví dụ: Bài 2.1 yêu cầu học sinh tính: a) 1/2 + 1/3; b) 2/5 - 1/4. Giải thích: a) Để cộng hai phân số 1/2 và 1/3, ta cần quy đồng mẫu số. Mẫu số chung nhỏ nhất của 2 và 3 là 6. Ta có: 1/2 = 3/6 và 1/3 = 2/6. Vậy, 1/2 + 1/3 = 3/6 + 2/6 = 5/6.
Bài 2.2: (Nêu yêu cầu bài tập và giải thích chi tiết cách giải).
...
Bài 3.1: (Nêu yêu cầu bài tập và giải thích chi tiết cách giải).
...
Ngoài sách giáo khoa, học sinh có thể tham khảo thêm các tài liệu sau để học tập và rèn luyện kỹ năng giải bài tập Toán 7:
Hy vọng rằng bài viết này đã cung cấp cho các em học sinh những kiến thức và kỹ năng cần thiết để giải quyết các bài tập trong mục 1 trang 77, 78, 79 SGK Toán 7 tập 2 Kết nối tri thức. Chúc các em học tập tốt!