Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng về mối liên hệ giữa độ dài các cạnh trong một tam giác. Chúng ta sẽ cùng tìm hiểu về bất đẳng thức tam giác và cách xác định cạnh lớn nhất, cạnh nhỏ nhất trong tam giác.
Nắm vững lý thuyết này là nền tảng để giải quyết các bài toán liên quan đến tam giác trong chương trình Toán 7 Kết nối tri thức.
Bất đẳng thức tam giác
Bất đẳng thức tam giác
Định lý. Trong một tam giác, tổng độ dài hai cạnh bất kỳ bao giờ cũng lớn hơn độ dài cạnh còn lại.
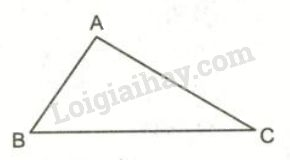

Trong một tam giác, hiệu độ dài hai cạnh bất kỳ bao giờ cũng nhỏ hơn độ dài cạnh còn lại
Nhận xét: Trong một tam giác, độ dài một cạnh bao giờ cũng lớn hơn hiệu độ dài hai cạnh còn lại và nhỏ hơn tổng độ dài của hai cạnh còn lại.
Trong tam giác \(ABC\), ta có:
\(|AB - AC| < BC < AB + AC\).
Trong hình học, tam giác là một hình đa giác có ba cạnh và ba góc. Việc hiểu rõ mối quan hệ giữa các cạnh của một tam giác là vô cùng quan trọng, không chỉ trong việc giải toán mà còn ứng dụng trong nhiều lĩnh vực thực tế. Bài viết này sẽ trình bày chi tiết về lý thuyết quan hệ giữa ba cạnh của một tam giác, dành cho học sinh lớp 7 chương trình Kết nối tri thức.
Bất đẳng thức tam giác là một trong những khái niệm cơ bản nhất trong hình học tam giác. Nó phát biểu rằng:
Cụ thể, nếu tam giác ABC có ba cạnh là a, b, c thì:
Ví dụ: Tam giác có các cạnh 3cm, 4cm, 5cm là một tam giác hợp lệ vì:
Ngược lại, tam giác có các cạnh 1cm, 2cm, 5cm không phải là một tam giác hợp lệ vì 1 + 2 < 5.
Trong một tam giác, cạnh lớn hơn đối diện với góc lớn hơn và cạnh nhỏ hơn đối diện với góc nhỏ hơn. Điều này có nghĩa là:
Chứng minh: (Chứng minh có thể được trình bày chi tiết bằng hình vẽ và các bước suy luận logic, nhưng ở đây chỉ nêu kết quả)
Để xác định cạnh lớn nhất và cạnh nhỏ nhất trong một tam giác, ta có thể sử dụng các phương pháp sau:
Bài 1: Cho tam giác ABC có AB = 5cm, BC = 7cm, AC = 9cm. Hãy xác định cạnh lớn nhất và cạnh nhỏ nhất của tam giác.
Giải:
Bài 2: Cho tam giác DEF có góc D = 60 độ, góc E = 80 độ, góc F = 40 độ. Hãy xác định cạnh lớn nhất và cạnh nhỏ nhất của tam giác.
Giải:
Lý thuyết quan hệ giữa ba cạnh của một tam giác có nhiều ứng dụng trong thực tế, ví dụ như:
Lý thuyết quan hệ giữa ba cạnh của một tam giác là một kiến thức nền tảng quan trọng trong hình học. Việc nắm vững lý thuyết này sẽ giúp bạn giải quyết các bài toán một cách hiệu quả và ứng dụng vào thực tế một cách linh hoạt. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán của mình.