Bài 1 trang 42 Vở thực hành Toán 8 tập 2 là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này giúp học sinh rèn luyện kỹ năng áp dụng các kiến thức đã học vào giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 1 trang 42 Vở thực hành Toán 8 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Các giá trị tương ứng của hai đại lượng x và y cho bởi các bảng sau. Đại lượng y có phải là một hàm số của x không?
Đề bài
Các giá trị tương ứng của hai đại lượng x và y cho bởi các bảng sau. Đại lượng y có phải là một hàm số của x không?
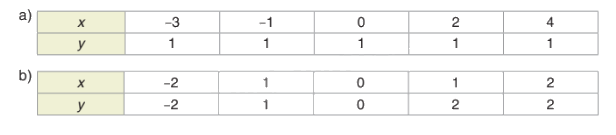
Phương pháp giải - Xem chi tiết
Quan sát nếu mỗi giá trị của x ta chỉ xác định được duy nhất một giá trị của y thì y là hàm số của x.
Lời giải chi tiết
a) Đại lượng y là hàm số của x vì với mỗi giá trị của x (thuộc tập hợp {-3; -1; 0; 2; 4}) ta luôn xác định được chỉ một giá trị tương ứng của y (y luôn bằng 1).
b) Đại lượng y không là hàm số của x vì với x = 1 ta xác định được hai giá trị tương ứng của y là y = 1 và y = 2.
Bài 1 trang 42 Vở thực hành Toán 8 tập 2 thường liên quan đến việc áp dụng các định lý, tính chất đã học trong chương trình hình học hoặc đại số. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững lý thuyết cơ bản và biết cách vận dụng linh hoạt các phương pháp giải phù hợp.
Để cung cấp lời giải chi tiết cho bài 1 trang 42 Vở thực hành Toán 8 tập 2, chúng ta cần biết nội dung cụ thể của bài tập. Tuy nhiên, dựa trên kinh nghiệm giải các bài tập tương tự, chúng ta có thể đưa ra một số hướng giải chung:
Đề bài: Cho hình bình hành ABCD. Gọi E là trung điểm của cạnh AB. Đường thẳng DE cắt AC tại I. Chứng minh rằng AI = IC.
Lời giải:
Để củng cố kiến thức và kỹ năng giải bài tập, học sinh nên luyện tập thêm các bài tập tương tự trong sách giáo khoa, sách bài tập và các nguồn tài liệu khác. Việc luyện tập thường xuyên sẽ giúp học sinh nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Bài 1 trang 42 Vở thực hành Toán 8 tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán. Bằng cách nắm vững lý thuyết, áp dụng phương pháp giải phù hợp và luyện tập thường xuyên, học sinh có thể tự tin giải quyết bài tập này một cách hiệu quả.