Bạn đang gặp khó khăn trong việc giải các bài tập trắc nghiệm Toán 8 trang 47 Vở thực hành? Đừng lo lắng, giaitoan.edu.vn sẽ cung cấp cho bạn lời giải chi tiết và dễ hiểu nhất.
Chúng tôi hiểu rằng việc học Toán đôi khi có thể gây khó khăn, đặc biệt là với các dạng bài tập trắc nghiệm. Vì vậy, chúng tôi đã tập hợp đội ngũ giáo viên giàu kinh nghiệm để giải đáp mọi thắc mắc của bạn.
Chọn phương án đúng trong mỗi câu sau:
Điền cụm từ thích hợp vào chỗ trống.
a) Hình thang cân là ............................................................................................ bằng nhau.
b) Hình thang có ....................................................................................... là hình thang cân.
c) Hai cạnh bên của hình thang cân .....................................................................................
d) Hình thang cân ABCD (AB // CD) có AD = ...................; AC = ..................; \(\widehat A = \).................. ; \(\widehat C = \)..................
Phương pháp giải:
- Sử dụng khái niệm hình thang cân: Hình thang cân là hình cân là hình thang có hai góc kề một đáy bằng nhau.
- Dựa vào tính chất của hình thang cân:
+ Định lí 1. Trong hình thang cân, hai cạnh bên bằng nhau.
+ Định lí 2. Trong hình thang cân, hai đường chéo bằng nhau.
- Dựa vào dấu hiệu nhận biết hình thang cân:
+ Định lí 3. Nếu một hình thang có hai đường chéo bằng nhau thì hình thang đó là hình thang cân.
Lời giải chi tiết:
a) Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
b) Hình thang có hai đường chéo bằng nhau là hình thang cân.
c) Hai cạnh bên của hình thang cân bằng nhau.
d) Hình thang cân ABCD (AB // CD) có \(AD = BC;AC = BD;\;\widehat A = \widehat B;\widehat C = \widehat D\).
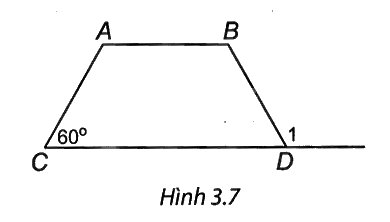
Cho hình thang ABCD cân (AB // CD) có \(\widehat C = {60^0}\) (H.3.7). Khi đó, số đo \(\widehat {{D_1}}\) bằng:
A. \(60^\circ \)
B. \(80^\circ \)
C. \(120^\circ \)
D. \(100^\circ \)
Phương pháp giải:
Sử dụng khái niệm hình thang cân: Hình thang cân là hình cân là hình thang có hai góc kề một đáy bằng nhau và tổng hai góc kề bù bằng \({180^0}\).
Lời giải chi tiết:
Vì ABCD là hình thang cân nên \(\widehat {ACD} = \widehat {BDC} = 60^\circ \).
Do đó \(\widehat {{D_1}} = 180^\circ - \widehat {BDC} = 180^\circ - 60^\circ = 120^\circ .\)
=> Chọn đáp án C.
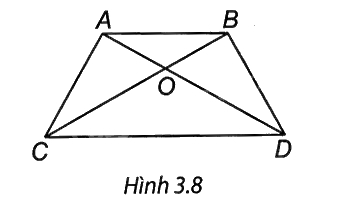
Cho hình thang ABCD có AB // CD, hai đường chéo AC và BD cắt nhau tại O sao cho OA = OB; OC = OD (H.3.8).
Trong các khẳng định sau, khẳng định sai là
A. BC = AD.
B. ABCD là hình thang cân.
C. AC = BD.
D. Tam giác AOC cân tại O.
Phương pháp giải:
- Dựa vào tính chất của hình thang cân:
+ Định lí 1. Trong hình thang cân, hai cạnh bên bằng nhau.
+ Định lí 2. Trong hình thang cân, hai đường chéo bằng nhau.
- Dựa vào dấu hiệu nhận biết hình thang cân:
+ Định lí 3. Nếu một hình thang có hai đường chéo bằng nhau thì hình thang đó là hình thang cân.
Lời giải chi tiết:
Ta có: OA = OB; OC = OD suy ra OA + OC = OB + OD
Khi đó AC = BD nên ABCD là hình thang cân. Do đó B, C đúng.
ABCD là hình thang cân nên hai cạnh bên bằng nhau nên BD = AC. Do đó A đúng.
Vì A, O, C thẳng hàng nên D là khẳng định sai.
=> Chọn đáp án D.
Chọn phương án đúng trong mỗi câu sau:
Điền cụm từ thích hợp vào chỗ trống.
a) Hình thang cân là ............................................................................................ bằng nhau.
b) Hình thang có ....................................................................................... là hình thang cân.
c) Hai cạnh bên của hình thang cân .....................................................................................
d) Hình thang cân ABCD (AB // CD) có AD = ...................; AC = ..................; \(\widehat A = \).................. ; \(\widehat C = \)..................
Phương pháp giải:
- Sử dụng khái niệm hình thang cân: Hình thang cân là hình cân là hình thang có hai góc kề một đáy bằng nhau.
- Dựa vào tính chất của hình thang cân:
+ Định lí 1. Trong hình thang cân, hai cạnh bên bằng nhau.
+ Định lí 2. Trong hình thang cân, hai đường chéo bằng nhau.
- Dựa vào dấu hiệu nhận biết hình thang cân:
+ Định lí 3. Nếu một hình thang có hai đường chéo bằng nhau thì hình thang đó là hình thang cân.
Lời giải chi tiết:
a) Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
b) Hình thang có hai đường chéo bằng nhau là hình thang cân.
c) Hai cạnh bên của hình thang cân bằng nhau.
d) Hình thang cân ABCD (AB // CD) có \(AD = BC;AC = BD;\;\widehat A = \widehat B;\widehat C = \widehat D\).
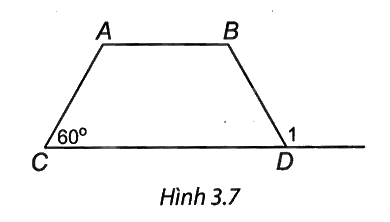
Cho hình thang ABCD cân (AB // CD) có \(\widehat C = {60^0}\) (H.3.7). Khi đó, số đo \(\widehat {{D_1}}\) bằng:
A. \(60^\circ \)
B. \(80^\circ \)
C. \(120^\circ \)
D. \(100^\circ \)
Phương pháp giải:
Sử dụng khái niệm hình thang cân: Hình thang cân là hình cân là hình thang có hai góc kề một đáy bằng nhau và tổng hai góc kề bù bằng \({180^0}\).
Lời giải chi tiết:
Vì ABCD là hình thang cân nên \(\widehat {ACD} = \widehat {BDC} = 60^\circ \).
Do đó \(\widehat {{D_1}} = 180^\circ - \widehat {BDC} = 180^\circ - 60^\circ = 120^\circ .\)
=> Chọn đáp án C.
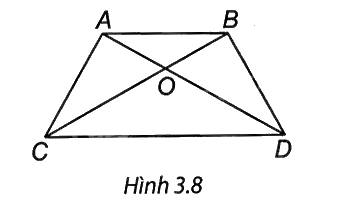
Cho hình thang ABCD có AB // CD, hai đường chéo AC và BD cắt nhau tại O sao cho OA = OB; OC = OD (H.3.8).
Trong các khẳng định sau, khẳng định sai là
A. BC = AD.
B. ABCD là hình thang cân.
C. AC = BD.
D. Tam giác AOC cân tại O.
Phương pháp giải:
- Dựa vào tính chất của hình thang cân:
+ Định lí 1. Trong hình thang cân, hai cạnh bên bằng nhau.
+ Định lí 2. Trong hình thang cân, hai đường chéo bằng nhau.
- Dựa vào dấu hiệu nhận biết hình thang cân:
+ Định lí 3. Nếu một hình thang có hai đường chéo bằng nhau thì hình thang đó là hình thang cân.
Lời giải chi tiết:
Ta có: OA = OB; OC = OD suy ra OA + OC = OB + OD
Khi đó AC = BD nên ABCD là hình thang cân. Do đó B, C đúng.
ABCD là hình thang cân nên hai cạnh bên bằng nhau nên BD = AC. Do đó A đúng.
Vì A, O, C thẳng hàng nên D là khẳng định sai.
=> Chọn đáp án D.
Trang 47 Vở thực hành Toán 8 thường chứa các bài tập trắc nghiệm liên quan đến các kiến thức đã học trong chương. Để giải quyết hiệu quả các bài tập này, học sinh cần nắm vững lý thuyết, hiểu rõ các định nghĩa và công thức liên quan.
Các câu hỏi trắc nghiệm trang 47 thường tập trung vào các dạng bài sau:
Để giúp các em học sinh hiểu rõ hơn, chúng ta sẽ đi vào giải chi tiết từng câu hỏi trắc nghiệm trong trang 47 Vở thực hành Toán 8.
Đề bài: Cho biểu thức A = (x + 2)(x - 2). Chọn đáp án đúng:
Giải:
Sử dụng hằng đẳng thức (a + b)(a - b) = a2 - b2, ta có:
A = (x + 2)(x - 2) = x2 - 22 = x2 - 4
Vậy đáp án đúng là B.
Đề bài: Cho hình bình hành ABCD. Gọi M là trung điểm của BC. Gọi N là giao điểm của AM và BD. Chọn đáp án đúng:
Giải:
Xét tam giác BCD, M là trung điểm của BC, N là giao điểm của AM và BD. Áp dụng định lý Menelaus cho tam giác BCD với đường thẳng AM, ta có:
(BM/MC) * (CA/AD) * (DN/NB) = 1
Vì BM = MC nên BM/MC = 1. Vì ABCD là hình bình hành nên CA = AD. Do đó:
1 * (CA/AD) * (DN/NB) = 1 => DN/NB = 1 => DN = NB
Vậy đáp án đúng là A.
Để giải nhanh các bài tập trắc nghiệm, bạn có thể áp dụng một số mẹo sau:
Giải bài tập trắc nghiệm không chỉ giúp bạn củng cố kiến thức đã học mà còn rèn luyện kỹ năng tư duy logic, khả năng phân tích và đánh giá vấn đề. Đây là những kỹ năng quan trọng không chỉ trong học tập mà còn trong cuộc sống.
Hy vọng với những hướng dẫn chi tiết và mẹo giải nhanh trên đây, các em học sinh sẽ tự tin hơn trong việc giải các câu hỏi trắc nghiệm trang 47 Vở thực hành Toán 8. Chúc các em học tập tốt!