Bài 6 trang 88 Vở thực hành Toán 8 tập 2 là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học về hình học, đặc biệt là các định lý liên quan đến tứ giác để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 6 trang 88 Vở thực hành Toán 8 tập 2, giúp các em học sinh hiểu rõ bản chất của bài toán và rèn luyện kỹ năng giải toán.
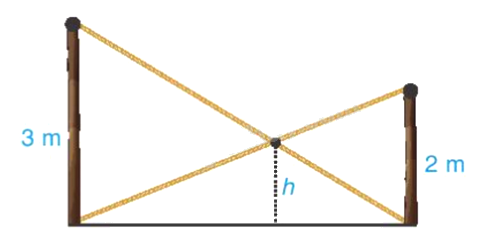
Có hai chiếc cột dựng thẳng đứng trên mặt đất với chiều cao lần lượt là 3m và 2m. Người ta nối hai sợi dây từ đỉnh cột này đến chân cột kia và hai sợi dây cắt nhau tại một điểm (H.9.25),
Đề bài
Có hai chiếc cột dựng thẳng đứng trên mặt đất với chiều cao lần lượt là 3m và 2m. Người ta nối hai sợi dây từ đỉnh cột này đến chân cột kia và hai sợi dây cắt nhau tại một điểm (H.9.25), hãy tính độ cao h của điểm đó so với mặt đất.
Phương pháp giải - Xem chi tiết
- Theo đề bài vẽ lại hình và đặt tên các điểm.
- Chứng minh các tam giác đồng dạng và suy ra các tỉ số đồng dạng để tính độ cao của h
Lời giải chi tiết
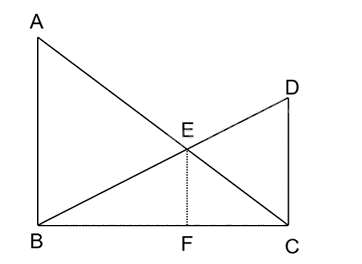
Hình 9.6
Kí hiệu các điểm như hình 9.6.
Ta có AB, EF, CD đôi một song song vì cùng vuông góc với BC.
Do đó, $\Delta DEF\backsim \Delta DAB$ và $\Delta BEF\backsim \Delta BCD$. Suy ra $\frac{EF}{AB}=\frac{DF}{DB}$ và $\frac{EF}{CD}=\frac{BF}{BD}$.
Do đó $\frac{EF}{CD}+\frac{EF}{AB}=\frac{BF}{BD}+\frac{DF}{DB}=1$, và suy ra $\frac{EF(AB+CD)}{AB.CD}=1$.
Vì vậy $h=EF=\frac{AB.CD}{AB+CD}=\frac{6}{5}=1,2$(m).
Bài 6 trang 88 Vở thực hành Toán 8 tập 2 thuộc chương trình học về tứ giác, một trong những kiến thức nền tảng của hình học lớp 8. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các định nghĩa, tính chất của các loại tứ giác đặc biệt như hình chữ nhật, hình thoi, hình vuông, hình bình hành và các dấu hiệu nhận biết chúng.
Bài 6 thường yêu cầu học sinh chứng minh một tứ giác là một loại tứ giác đặc biệt nào đó dựa trên các thông tin đã cho về độ dài cạnh, góc hoặc đường chéo. Đôi khi, bài toán cũng yêu cầu tính độ dài cạnh, góc hoặc diện tích của tứ giác đó.
Để giải bài 6 trang 88 Vở thực hành Toán 8 tập 2, học sinh có thể áp dụng các phương pháp sau:
Giả sử đề bài yêu cầu chứng minh tứ giác ABCD là hình bình hành, với A(0;0), B(2;1), C(3;3), D(1;2). Ta có thể thực hiện như sau:
Ngoài dạng bài chứng minh tứ giác là một loại tứ giác đặc biệt, bài 6 trang 88 Vở thực hành Toán 8 tập 2 còn có thể xuất hiện các dạng bài tập sau:
Khi giải bài tập về tứ giác, học sinh cần lưu ý những điều sau:
Để rèn luyện kỹ năng giải bài tập về tứ giác, học sinh có thể tham khảo các bài tập tương tự trong sách giáo khoa, sách bài tập và các trang web học toán online.
Bài 6 trang 88 Vở thực hành Toán 8 tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về tứ giác. Bằng cách nắm vững các kiến thức nền tảng, áp dụng các phương pháp giải phù hợp và rèn luyện thường xuyên, học sinh có thể giải quyết bài toán này một cách hiệu quả và đạt kết quả tốt trong học tập.