Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập Toán 8. Chúng tôi hiểu rằng việc giải các bài tập trắc nghiệm có thể gặp nhiều khó khăn, đặc biệt là với những học sinh mới bắt đầu làm quen với phương pháp này.
Bài viết này sẽ giúp bạn giải quyết triệt để các câu hỏi trắc nghiệm trang 44 Vở thực hành Toán 8, đồng thời cung cấp kiến thức nền tảng vững chắc để bạn tự tin hơn trong các bài kiểm tra và kỳ thi sắp tới.
Chọn phương án đúng trong mỗi câu sau:
Cho tứ giác ABCD có \(\widehat A = 80^\circ ,\widehat D = 40^\circ ,\widehat C = 95^\circ \). Khi đó góc B có số đo là
A. \(60^\circ \).
B. \(45^\circ \).
C. \(135^\circ \).
D. \(145^\circ \).
Phương pháp giải:
Sử dụng định lí tổng các góc của tứ giác: Tổng các góc của một tứ giác bằng \({360^0}\).
Lời giải chi tiết:
Tổng các góc của một tứ giác bằng \(360^\circ \) nên ta có
\(\widehat A + \widehat B + \widehat C + \widehat D = {360^0}\) hay \({80^0} + \widehat B + {95^0} + {40^0} = {360^0}\)
Do đó \(\widehat B = {145^0}.\)
=> Chọn đáp án D.
Chọn phương án đúng trong mỗi câu sau:
Cho tứ giác ABCD có \(\widehat A = 80^\circ ,\widehat D = 40^\circ ,\widehat C = 95^\circ \). Khi đó góc B có số đo là
A. \(60^\circ \).
B. \(45^\circ \).
C. \(135^\circ \).
D. \(145^\circ \).
Phương pháp giải:
Sử dụng định lí tổng các góc của tứ giác: Tổng các góc của một tứ giác bằng \({360^0}\).
Lời giải chi tiết:
Tổng các góc của một tứ giác bằng \(360^\circ \) nên ta có
\(\widehat A + \widehat B + \widehat C + \widehat D = {360^0}\) hay \({80^0} + \widehat B + {95^0} + {40^0} = {360^0}\)
Do đó \(\widehat B = {145^0}.\)
=> Chọn đáp án D.
Chọn phương án đúng.
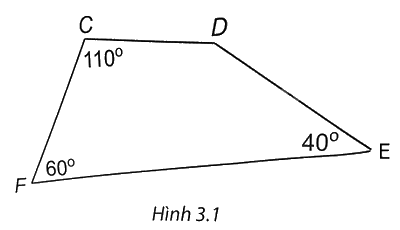
Cho tứ giác CDEF có số đo các góc như trên Hình 3.1. Khi đó số đo góc D là
A. \(x = 105^\circ \)
B. \(x = 140^\circ \)
C. \(x = 150^\circ \)
D. \(x = 120^\circ \)
Phương pháp giải:
Sử dụng định lí tổng các góc của tứ giác: Tổng các góc của một tứ giác bằng \({360^0}\).
Lời giải chi tiết:
Tổng các góc của một tứ giác bằng \(360^\circ \) nên xét tứ giác \(CDEF\) ta có
\(\widehat C + \widehat D + \widehat E + \widehat F = {360^0}\) hay \({110^0} + \widehat D + {40^0} + {60^0} = {360^0}\)
Do đó \(\widehat D = 150^\circ \).
=> Chọn đáp án C.
Chọn phương án đúng.
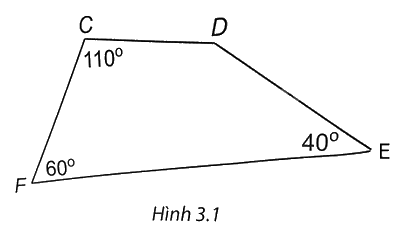
Cho tứ giác CDEF có số đo các góc như trên Hình 3.1. Khi đó số đo góc D là
A. \(x = 105^\circ \)
B. \(x = 140^\circ \)
C. \(x = 150^\circ \)
D. \(x = 120^\circ \)
Phương pháp giải:
Sử dụng định lí tổng các góc của tứ giác: Tổng các góc của một tứ giác bằng \({360^0}\).
Lời giải chi tiết:
Tổng các góc của một tứ giác bằng \(360^\circ \) nên xét tứ giác \(CDEF\) ta có
\(\widehat C + \widehat D + \widehat E + \widehat F = {360^0}\) hay \({110^0} + \widehat D + {40^0} + {60^0} = {360^0}\)
Do đó \(\widehat D = 150^\circ \).
=> Chọn đáp án C.
Trang 44 Vở thực hành Toán 8 thường chứa các bài tập trắc nghiệm liên quan đến các chủ đề đã học trong chương. Để giải quyết hiệu quả các bài tập này, trước hết, bạn cần nắm vững kiến thức lý thuyết và các công thức liên quan. Sau đó, hãy đọc kỹ đề bài, xác định rõ yêu cầu và các dữ kiện đã cho.
Câu 1: Rút gọn biểu thức: A = (x + 2)/(x - 1)
Lời giải: Biểu thức A = (x + 2)/(x - 1) đã là phân thức tối giản. Do đó, đáp án đúng là...
Câu 2: Giải phương trình: 2x + 3 = 7
Lời giải:
Do đó, đáp án đúng là x = 2.
Ngoài Vở thực hành Toán 8, bạn có thể tham khảo thêm các tài liệu sau để học Toán 8 hiệu quả hơn:
Hy vọng rằng với hướng dẫn chi tiết và dễ hiểu này, bạn sẽ tự tin hơn trong việc giải các câu hỏi trắc nghiệm trang 44 Vở thực hành Toán 8. Chúc bạn học tập tốt và đạt kết quả cao trong các kỳ thi sắp tới!