Bài 6 trang 115 Vở thực hành Toán 8 tập 2 là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về hình học để giải quyết các vấn đề thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 6 trang 115 VBT Toán 8 tập 2, giúp các em học sinh hiểu rõ bản chất bài toán và tự tin làm bài.
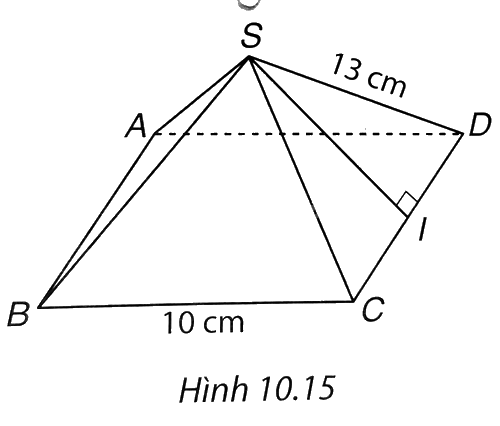
Cho hình chóp tứ giác đều S.ABCD có độ dài cạnh bên bằng 13 cm, cạnh đáy bằng 10 cm như Hình 10.15.
Đề bài
Cho hình chóp tứ giác đều S.ABCD có độ dài cạnh bên bằng 13 cm, cạnh đáy bằng 10 cm như Hình 10.15.
a) Tính diện tích xung quanh của hình chóp.
b) Tính diện tích toàn phần của hình chóp.
Phương pháp giải - Xem chi tiết
- Tính độ dài trung đoạn, ta tính được diện tích xung quanh.
- Tính diện tích đáy của hình chóp, tính diện tích toàn phần bằng diện tích xung quanh + diện tích đáy.
Lời giải chi tiết
a) CI = CD:2 = 10:3 = 5 (cm).
\(\Delta SIC\) vuông tại I nên theo định lí Pythagore, ta có:
SI2 + IC2 = SC2
SI2 + 522 = 132
SI2 = 132 – 52 = 122
Suy ra SI = 12.
Diện tích xung quanh của hình chóp S.ABCD là:
\({S_{xq}} = p.d = \frac{{10.4}}{2}.12 = 240\left( {c{m^2}} \right)\)
Diện tích đáy của hình chóp S.ABCD là Sđáy = 102 = 100 (cm2).
Diện tích toàn phần của hình chóp S.ABCD là:
Stp = Sxq + Sđáy = 240 + 100 = 340 (cm2).
Bài 6 trang 115 Vở thực hành Toán 8 tập 2 thuộc chương trình học về tứ giác. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về:
Để giải bài 6 trang 115 Vở thực hành Toán 8 tập 2, chúng ta cần phân tích kỹ đề bài và xác định yêu cầu của bài toán. Sau đó, áp dụng các kiến thức và phương pháp giải phù hợp để tìm ra đáp án chính xác.
Đề bài: (Giả sử đề bài là: Cho hình thang ABCD (AB // CD). Gọi M, N lần lượt là trung điểm của AD và BC. Chứng minh rằng MN // AB // CD và MN = (AB + CD) / 2)
Lời giải:
Xét tam giác ADC, M là trung điểm của AD và MN cắt DC tại I. Theo định lý Thales, ta có: DI/IC = AM/MD = 1. Suy ra DI = IC, tức là I là trung điểm của DC.
Tương tự, xét tam giác BCD, N là trung điểm của BC và MN cắt DC tại I. Theo định lý Thales, ta có: BI/IC = BN/NC = 1. Suy ra BI = IC, tức là I là trung điểm của DC.
Vậy, MN là đường trung bình của hình thang ABCD, do đó MN // AB // CD.
Vì MN là đường trung bình của hình thang ABCD, ta có: MN = (AB + CD) / 2.
Ngoài bài 6 trang 115, Vở thực hành Toán 8 tập 2 còn có nhiều bài tập tương tự về tứ giác. Để giải các bài tập này, học sinh có thể áp dụng các phương pháp sau:
Để củng cố kiến thức về tứ giác, các em học sinh có thể tự giải các bài tập sau:
Bài 6 trang 115 Vở thực hành Toán 8 tập 2 là một bài tập quan trọng giúp học sinh hiểu rõ hơn về tứ giác và các tính chất của nó. Hy vọng với lời giải chi tiết và phương pháp giải được trình bày ở trên, các em học sinh sẽ tự tin hơn khi làm bài tập Toán 8.