Bài 6 trang 94 Vở thực hành Toán 8 tập 2 là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học về hình học, đặc biệt là các định lý liên quan đến tứ giác để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 6 trang 94 Vở thực hành Toán 8 tập 2, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Chú cún bị xích bởi một sợi dây dài 6m để canh một mảnh vườn giới hạn bởi các điểm A, B, E, F, D trong hình vuông ABCD có cạnh 5m như Hình 9.44.
Đề bài
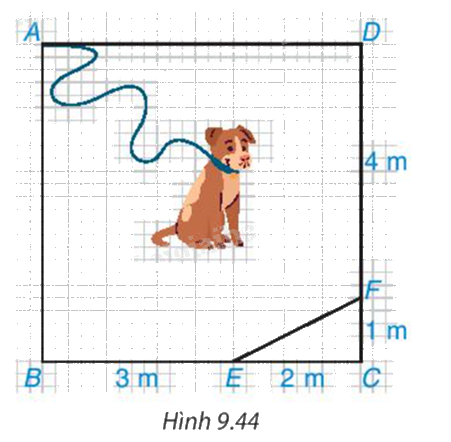
Chú cún bị xích bởi một sợi dây dài 6m để canh một mảnh vườn giới hạn bởi các điểm A, B, E, F, D trong hình vuông ABCD có cạnh 5m như Hình 9.44. Đầu xích buộc cố định tại điểm A của mảnh vườn. Hỏi chú cún có thể chạy đến tất cả các điểm của mảnh vườn mình phải canh không?
Phương pháp giải - Xem chi tiết
Áp dụng định lí Pythagore trong tam giác vuông.
Lời giải chi tiết
Áp dụng định lí Pythagore cho tam giác vuông ADF, ta có:
AF2 = AD2 + DF2 = 52+ 42 = 41, hay AF = $\sqrt{41}$ (m).
Như vậy AF > 6 m. Do đó, chú Cún không thể đến được điểm F. Vì vậy, chú Cún không thể đến được tất cả các điểm trong mảnh vườn.
Bài 6 trang 94 Vở thực hành Toán 8 tập 2 thường xoay quanh việc chứng minh một tứ giác là hình gì (hình bình hành, hình chữ nhật, hình thoi, hình vuông) dựa trên các điều kiện cho trước. Đôi khi, bài toán yêu cầu tính độ dài cạnh, số đo góc hoặc diện tích của tứ giác đó.
Để giải quyết bài toán liên quan đến tứ giác, học sinh cần nắm vững các kiến thức sau:
(Giả sử bài toán cụ thể là: Cho hình bình hành ABCD, gọi E là trung điểm của cạnh AB. Gọi F là giao điểm của DE và AC. Chứng minh: a) Tam giác ADE = Tam giác BCE. b) AF = FC.)
Xét tam giác ADE và tam giác BCE, ta có:
Vậy, tam giác ADE = tam giác BCE (g.c.g)
Do tam giác ADE = tam giác BCE (cmt) nên DE = CE.
Xét tam giác AFC và tam giác DFE, ta có:
Ta có: DE cắt AC tại F. Vì tam giác ADE = tam giác BCE nên AD = BC. Do ABCD là hình bình hành nên AD = BC. Xét tam giác ADF và tam giác CBF, ta có:
Vậy, tam giác ADF = tam giác CBF (g.c.g) suy ra AF = CF.
Ngoài bài toán trên, còn rất nhiều dạng bài tập tương tự về tứ giác. Để giải tốt các bài tập này, học sinh cần:
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập về tứ giác, học sinh có thể tham khảo thêm các bài tập sau:
Bài 6 trang 94 Vở thực hành Toán 8 tập 2 là một bài tập quan trọng giúp học sinh hiểu rõ hơn về các kiến thức về tứ giác. Hy vọng với lời giải chi tiết và phương pháp giải bài tập được trình bày trên đây, các em học sinh sẽ tự tin hơn khi làm bài tập Toán 8.