Bài 12 trang 128 Vở thực hành Toán 8 tập 2 là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học về hình học, đặc biệt là các tính chất của hình thang cân để giải quyết các vấn đề thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 12 trang 128 Vở thực hành Toán 8 tập 2, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho tam giác ABC không phải là tam giác vuông, có các đường cao BE, CF cắt nhau tại điểm H
Đề bài
Cho tam giác ABC không phải là tam giác vuông, có các đường cao BE, CF cắt nhau tại điểm H
a) Giả sử ABC là tam giác nhọn. Chứng minh rằng ΔABE $\backsim $ ΔACF , từ đó suy ra ΔAEF $\backsim $ ΔABC
b) Cho biết AB = 10 cm, BC = 15 cm và BE = 8 cm. Tính EF
Phương pháp giải - Xem chi tiết
a) Xét tam giác vuông ABE (vuông tại E) và tam giác vuông ACF (vuông tại F) có góc A chung => ΔABE $\backsim $ ΔACF (c.g.c)
b) Sử dụng các tỉ số đồng dạng của hai tam giác để tính EF
Lời giải chi tiết
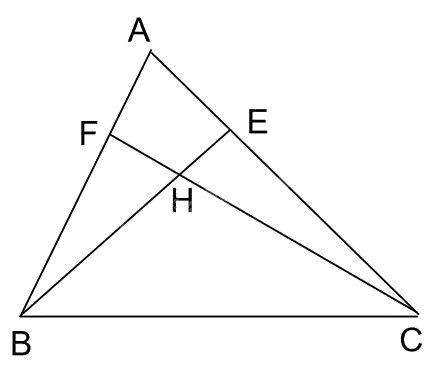
a) Khi tam giác ABC nhọn, ta có hình bên.
Xét tam giác vuông ABE (vuông tại E) và tam giác vuông ACF (vuông tại F) có góc A chung nên ΔABE $\backsim $ ΔACF
=> $\frac{AB}{AC}=\frac{A\text{E}}{AF}$
Xét tam giác AEF và tam giác ABC có: A chung và $\frac{AB}{AC}=\frac{A\text{E}}{AF}$
=> \(\Delta AEF\backsim \Delta ABC\)(c.g.c)
Khi tam giác ABC là tam giác tù, chẳng hạn góc A tù hoặc góc B tù, tương ứng ta có hai hình sau (HS tự vẽ)
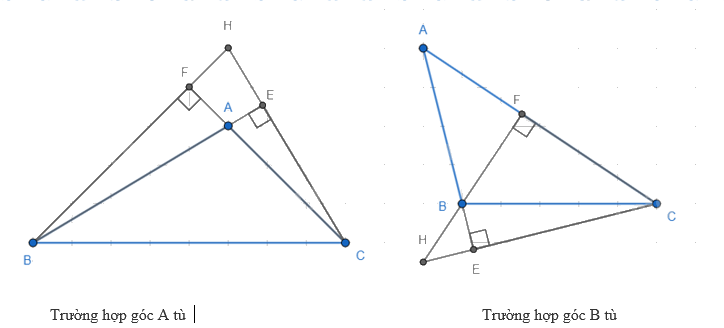
Chứng minh tương tự, ta thấy kết quả vẫn đúng.
b) Theo định lí Pythagore, trong tam giác vuông ABE, ta có:
\(A{{B}^{2}}=A{{E}^{2}}+B{{E}^{2}} \Rightarrow A{{E}^{2}}=A{{B}^{2}}-B{{E}^{2}} \\ ={{10}^{2}}-{{8}^{2}}=36\Rightarrow AE=6cm \)
Theo kết quả câu a), ta có
\(\Delta AEF\backsim \Delta ABC\Rightarrow \frac{EF}{AE}=\frac{BC}{AB}\Rightarrow EF=\frac{BC.AE}{AB}=\frac{15.6}{10}=9(cm)\)
Trả lời: EF = 9cm.
Cho hình thang cân ABCD (AB // CD), có AD = BC. Gọi E là giao điểm của AC và BD. Chứng minh rằng:
Để giải bài tập này, chúng ta cần dựa vào các tính chất của hình thang cân và tam giác cân.
Xét tam giác ADC và tam giác BCD, ta có:
Do đó, tam giác ADC bằng tam giác BCD (c-c-c).
Vì tam giác ADC bằng tam giác BCD (cmt) nên góc DAC = góc DBC.
Xét tam giác AED và tam giác BEC, ta có:
Do đó, tam giác AED bằng tam giác BEC (g-c-g).
Vì tam giác AED bằng tam giác BEC (cmt) nên:
Vậy, ta đã chứng minh được EA = EB và DE = EC.
Khi giải bài tập hình học, việc vẽ hình chính xác và đầy đủ là vô cùng quan trọng. Hình vẽ giúp chúng ta dễ dàng hình dung được bài toán và tìm ra hướng giải quyết.
Bài tập này là một ứng dụng quan trọng của các tính chất của hình thang cân. Ngoài ra, chúng ta còn có thể sử dụng các tính chất của tam giác cân để giải quyết các bài tập tương tự.
Để củng cố kiến thức, các em có thể tự giải các bài tập sau:
Bài 12 trang 128 Vở thực hành Toán 8 tập 2 là một bài tập điển hình về hình thang cân. Việc nắm vững các tính chất của hình thang cân và tam giác cân sẽ giúp các em giải quyết bài tập này một cách dễ dàng và hiệu quả.
Để hiểu rõ hơn về bài tập này, các em có thể tham khảo thêm các kiến thức sau:
| Khái niệm | Định nghĩa |
|---|---|
| Hình thang cân | Hình thang có hai cạnh đáy song song và hai cạnh bên bằng nhau. |
| Tam giác cân | Tam giác có hai cạnh bằng nhau. |
Hy vọng với lời giải chi tiết này, các em học sinh sẽ hiểu rõ hơn về bài 12 trang 128 Vở thực hành Toán 8 tập 2 và tự tin hơn trong quá trình học tập.