Bài 6 trang 103 Vở thực hành Toán 8 tập 2 là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về hình học để giải quyết các vấn đề thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 6 trang 103 Vở thực hành Toán 8 tập 2, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho tam giác ABC vuông tại A có đường cao AH. Gọi M,N lần lượt là các điểm trên các đoạn thẳng AB, AH sao cho AM = 2.MB, AN = $\frac{1}{2}$NH.
Đề bài
Cho tam giác ABC vuông tại A có đường cao AH. Gọi M,N lần lượt là các điểm trên các đoạn thẳng AB, AH sao cho AM = 2.MB, AN = $\frac{1}{2}$NH.
Chứng minh rằng $\Delta CAN\backsim \Delta CBM$ và $\Delta CHN\backsim \Delta CAM$.
Phương pháp giải - Xem chi tiết
Chứng minh \(\Delta CAH\backsim \Delta CBA\) => $\frac{CA}{CB}=\frac{AH}{BA}=\frac{AN}{CA}$ và $\widehat{CAH}=\widehat{CBA}$.
Chứng minh $\Delta CAN\backsim \Delta CBM$ và $\Delta CHN\backsim \Delta CAM$ dựa vào tỉ số cạnh tương ứng và góc xen giữa bằng nhau.
Lời giải chi tiết
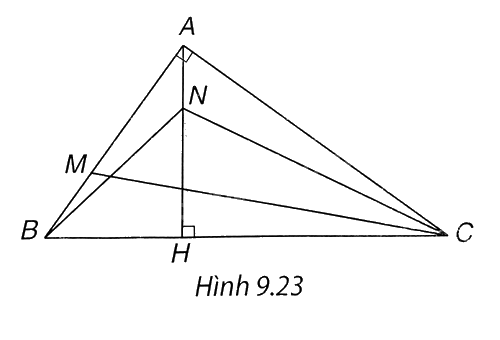
(H.9.23). Hai tam giác vuông CAH (vuông tại H) và CBA (vuông tại A) có góc C chung. Do đó \(\Delta CAH\backsim \Delta CBA\) (một cặp góc nhọn bằng nhau).
Suy ra $\frac{CA}{CB}=\frac{AH}{BA}=\frac{AN}{CA}$ và $\widehat{CAH}=\widehat{CBA}$.
Hai tam giác CAN và CBM có:
$\frac{CA}{CB}=\frac{AN}{BM}$ (theo chứng minh trên),
$\widehat{CBM}=\widehat{CAH}=\widehat{CBA}=\widehat{CBN}$ (theo chứng minh trên).
Vậy $\Delta CAN\backsim \Delta CBM$ (c.g.c).
Hai tam giác vuông CHN (vuông tại H) và CAM (vuông tại A) có:
$\frac{HC}{AC}=\frac{HA}{AB}=\frac{HN}{AM}$ (vì $\Delta CAH\backsim \Delta CBA$).
Vậy $\Delta CHN\backsim \Delta CAM$ (cạnh góc vuông – cạnh góc vuông)
Bài 6 trang 103 Vở thực hành Toán 8 tập 2 thuộc chương trình học về tứ giác. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về:
Bài tập 6 thường yêu cầu học sinh:
Để giải bài 6 trang 103 Vở thực hành Toán 8 tập 2, chúng ta cần phân tích kỹ đề bài, xác định các yếu tố đã cho và yếu tố cần tìm. Sau đó, vận dụng các kiến thức và phương pháp giải phù hợp để tìm ra đáp án chính xác.
Ví dụ minh họa:
Giả sử đề bài yêu cầu tính góc B của tứ giác ABCD, biết góc A = 80 độ, góc C = 100 độ, và góc D = 90 độ.
Lời giải:
Trong tứ giác ABCD, tổng các góc bằng 360 độ. Do đó:
∠A + ∠B + ∠C + ∠D = 360°
80° + ∠B + 100° + 90° = 360°
∠B = 360° - (80° + 100° + 90°)
∠B = 90°
Vậy, góc B của tứ giác ABCD bằng 90 độ.
Ngoài dạng bài tập tính góc, cạnh, còn có các dạng bài tập khác như:
Bài 6 trang 103 Vở thực hành Toán 8 tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về tứ giác. Bằng cách nắm vững lý thuyết, luyện tập thường xuyên và áp dụng các phương pháp giải phù hợp, các em học sinh có thể tự tin giải quyết bài tập này và đạt kết quả tốt trong môn Toán.