Chào mừng bạn đến với giaitoan.edu.vn! Chúng tôi cung cấp lời giải chi tiết và dễ hiểu cho các câu hỏi trắc nghiệm trang 96 Vở thực hành Toán 8 tập 2. Mục tiêu của chúng tôi là giúp các em học sinh nắm vững kiến thức và tự tin giải quyết các bài toán.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi cam kết mang đến cho bạn những lời giải chính xác và đầy đủ nhất.
Chọn phương án đúng trong mỗi câu sau.
Khẳng định nào dưới đây là đúng?
A. Hai tam giác vuông có tổng hai góc nhọn bằng nhau thì đồng dạng với nhau.
B. Hai tam giác vuông có một cặp cạnh bằng nhau thì đồng dạng với nhau.
C. Hai tam giác vuông có diện tích bằng nhau thì đồng dạng với nhau.
D. Hai tam giác vuông có một cặp góc nhọn bằng nhau thì đồng dạng với nhau.
Phương pháp giải:
Dựa vào các trường hợp đồng dạng của hai tam giác vuông.
Lời giải chi tiết:
Theo định lí 1: Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
=> Chọn đáp án D.
Cho tam giác ABC vuông tại A và tam giác DEF vuông tại D. Điều kiện nào dưới đây không suy ra $\Delta ABC\backsim \Delta DEF$?
A. $\widehat{B}=\widehat{E}$.
B. $\frac{AB}{DE}=\frac{AC}{DF}$.
C. $\frac{AB}{DE}=\frac{BC}{EF}$.
D. $\widehat{C}=\widehat{E}$.
Phương pháp giải:
Dựa vào các điều kiện để hai tam giác vuông đồng dạng với nhau.
Lời giải chi tiết:
Để tam giác $\Delta ABC\backsim \Delta DEF$ đồng dạng thì
TH1. $\widehat{B}=\widehat{E}$ hoặc $\widehat{C}=\widehat{F}$.
TH2. $\frac{AB}{DE}=\frac{AC}{DF}$.
TH3. $\frac{AB}{DE}=\frac{BC}{EF}$.
=> Chọn đáp án D.
Cho tam giác ABC vuông tại A và có đường cao AH. Khẳng định nào sau đây là đúng?
A. $\Delta ABC\backsim \Delta HAB$.
B. $\Delta ABC\backsim \Delta HCA$.
C. $\Delta HAB\backsim \Delta HAC$.
D. $\Delta ACB\backsim \Delta HCA$.
Phương pháp giải:
Dựa vào các trường hợp đồng dạng của hai tam giác vuông.
Lời giải chi tiết:
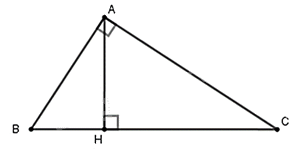
Xét tam giác $\Delta ACB\backsim \Delta HCA$ có:
$\widehat{A}=\widehat{H}={{90}^{0}}$
$\widehat{C}$ chung
=> Tam giác $\Delta ACB\backsim \Delta HCA$.
=> Chọn đáp án D.
Chọn phương án đúng trong mỗi câu sau.
Khẳng định nào dưới đây là đúng?
A. Hai tam giác vuông có tổng hai góc nhọn bằng nhau thì đồng dạng với nhau.
B. Hai tam giác vuông có một cặp cạnh bằng nhau thì đồng dạng với nhau.
C. Hai tam giác vuông có diện tích bằng nhau thì đồng dạng với nhau.
D. Hai tam giác vuông có một cặp góc nhọn bằng nhau thì đồng dạng với nhau.
Phương pháp giải:
Dựa vào các trường hợp đồng dạng của hai tam giác vuông.
Lời giải chi tiết:
Theo định lí 1: Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
=> Chọn đáp án D.
Cho tam giác ABC vuông tại A và tam giác DEF vuông tại D. Điều kiện nào dưới đây không suy ra $\Delta ABC\backsim \Delta DEF$?
A. $\widehat{B}=\widehat{E}$.
B. $\frac{AB}{DE}=\frac{AC}{DF}$.
C. $\frac{AB}{DE}=\frac{BC}{EF}$.
D. $\widehat{C}=\widehat{E}$.
Phương pháp giải:
Dựa vào các điều kiện để hai tam giác vuông đồng dạng với nhau.
Lời giải chi tiết:
Để tam giác $\Delta ABC\backsim \Delta DEF$ đồng dạng thì
TH1. $\widehat{B}=\widehat{E}$ hoặc $\widehat{C}=\widehat{F}$.
TH2. $\frac{AB}{DE}=\frac{AC}{DF}$.
TH3. $\frac{AB}{DE}=\frac{BC}{EF}$.
=> Chọn đáp án D.
Cho tam giác ABC vuông tại A và có đường cao AH. Khẳng định nào sau đây là đúng?
A. $\Delta ABC\backsim \Delta HAB$.
B. $\Delta ABC\backsim \Delta HCA$.
C. $\Delta HAB\backsim \Delta HAC$.
D. $\Delta ACB\backsim \Delta HCA$.
Phương pháp giải:
Dựa vào các trường hợp đồng dạng của hai tam giác vuông.
Lời giải chi tiết:
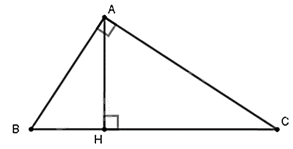
Xét tam giác $\Delta ACB\backsim \Delta HCA$ có:
$\widehat{A}=\widehat{H}={{90}^{0}}$
$\widehat{C}$ chung
=> Tam giác $\Delta ACB\backsim \Delta HCA$.
=> Chọn đáp án D.
Trang 96 Vở thực hành Toán 8 tập 2 thường chứa các bài tập trắc nghiệm liên quan đến các chủ đề đã học trong chương. Các dạng bài tập thường gặp bao gồm: nhận biết các khái niệm, vận dụng kiến thức vào giải quyết bài toán thực tế, và các bài tập kết hợp nhiều kiến thức khác nhau. Việc giải các bài tập trắc nghiệm này không chỉ giúp học sinh củng cố kiến thức mà còn rèn luyện kỹ năng làm bài thi.
Để giải các bài tập dạng này, học sinh cần nắm vững định nghĩa, tính chất của các khái niệm đã học. Đọc kỹ đề bài, xác định đúng khái niệm được hỏi và lựa chọn đáp án phù hợp.
Đối với các bài tập này, học sinh cần vận dụng kiến thức đã học để phân tích bài toán, tìm ra phương pháp giải phù hợp và thực hiện các phép tính chính xác.
Đây là dạng bài tập khó hơn, đòi hỏi học sinh phải có khả năng tổng hợp kiến thức từ nhiều chủ đề khác nhau. Học sinh cần phân tích bài toán một cách kỹ lưỡng, xác định các kiến thức liên quan và kết hợp chúng để giải quyết bài toán.
Câu hỏi: Đa thức nào sau đây là kết quả của phép nhân (x + 2)(x - 3)?
Lời giải:
(x + 2)(x - 3) = x(x - 3) + 2(x - 3) = x2 - 3x + 2x - 6 = x2 - x - 6
Vậy đáp án đúng là B. x2 - x - 6
Ngoài Vở thực hành Toán 8 tập 2, bạn có thể tham khảo thêm các tài liệu sau:
Việc giải các câu hỏi trắc nghiệm trang 96 Vở thực hành Toán 8 tập 2 là một bước quan trọng trong quá trình học Toán 8. Hy vọng với những hướng dẫn và ví dụ minh họa trên, các em học sinh sẽ tự tin hơn trong việc giải quyết các bài tập trắc nghiệm và đạt kết quả tốt trong môn Toán.