Bài 11 trang 127 Vở thực hành Toán 8 tập 2 là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về các định lý, tính chất của hình học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 11 trang 127 Vở thực hành Toán 8 tập 2, giúp các em học sinh hiểu rõ bản chất của bài toán và rèn luyện kỹ năng giải toán.
Cho tam giác ABC cân tại đỉnh A. Hai đường phân giác BE và CF của tam giác ABC cắt nhau tại điểm I. Chứng minh rằng
Đề bài
Cho tam giác ABC cân tại đỉnh A. Hai đường phân giác BE và CF của tam giác ABC cắt nhau tại điểm I. Chứng minh rằng
a) ΔBIC $\backsim $ ΔEIF
b) $F{{B}^{2}}=FI.FC$
c) Cho biết AB = 6cm, BC = 3 cm. Tính EF
Phương pháp giải - Xem chi tiết
a) Sử dụng định lí Thales đảo chứng minh EF // BC
b) Sử dụng các tỉ số đồng dạng của hai tam giác để chứng minh $F{{B}^{2}}=FI.FC$
c) Dựa vào định lí Thales cho EF // BC, ta có các tỉ số bằng nhau suy ra độ dài EF.
Lời giải chi tiết
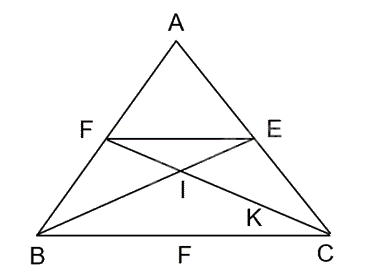
a) Do BE là đường phân giác của góc B nên $\widehat{{{B}_{1}}}=\widehat{{{B}_{2}}}$, ta có: $\frac{EA}{EC}=\frac{BA}{BC}$ (1).
Tương tự với đường phân giác CF, ta có: $\frac{FA}{FB}=\frac{CA}{CB}$ (2).
Bởi vậy, từ (1) và (2) ta suy ra $\frac{EA}{EC}=\frac{FA}{FB}$, nghĩa là EF định ra trên hai cạnh AB và AC những đoạn thẳng tương ứng tỉ lệ. Do đó theo định lí Thales đảo ta có EF // BC. Từ đó suy ra $\Delta BIC\backsim \Delta EIF$ (đpcm).
b) Hai tam giác BFI và CFB có $\widehat{F}$ chung, $\widehat{{{B}_{1}}}=\frac{\widehat{ABC}}{2}=\frac{\widehat{ACB}}{2}=\widehat{{{C}_{2}}}$.
Do đó $\Delta BFI\backsim \Delta CFB\Rightarrow \frac{FB}{FC}=\frac{FI}{FB}\Rightarrow F{{B}^{2}}=FI.FC$ (đpcm).
c) Ta có EF // BC (chứng minh trên). Do đó: $\frac{BC}{EF}=\frac{AB}{AF}\Rightarrow \frac{BC}{EF}=\frac{\left( AF+FB \right)}{AF}=1+\frac{BC}{AB}=1+\frac{3}{6}=\frac{3}{2}$.
Từ đó suy ra EF = 3: $\frac{3}{2}$ = 2 (cm).
Bài 11 trang 127 Vở thực hành Toán 8 tập 2 thuộc chương trình học về tứ giác. Để giải bài tập này, học sinh cần nắm vững các kiến thức sau:
Đề bài: (Đề bài cụ thể của bài 11 sẽ được chèn vào đây. Ví dụ: Cho tứ giác ABCD nội tiếp đường tròn. Biết góc A = 80 độ, góc C = 100 độ. Tính số đo các góc B và D.)
Lời giải:
Để hiểu rõ hơn về cách giải bài tập về tứ giác nội tiếp, chúng ta cùng xem xét một ví dụ minh họa sau:
Ví dụ: Cho tứ giác ABCD nội tiếp đường tròn. Biết ∠A = 70 độ, ∠B = 110 độ. Tính số đo các góc C và D.
Lời giải:
Dưới đây là một số bài tập tương tự để các em luyện tập:
Bài 11 trang 127 Vở thực hành Toán 8 tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về tứ giác nội tiếp. Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các em học sinh sẽ hiểu rõ hơn về bài toán và tự tin giải các bài tập tương tự.
| Công thức | Mô tả |
|---|---|
| Tổng các góc trong tứ giác | ∠A + ∠B + ∠C + ∠D = 360° |
| Tứ giác nội tiếp | ∠A + ∠C = 180° và ∠B + ∠D = 180° |