Chào mừng các em học sinh đến với lời giải chi tiết bài 2 trang 61 Vở thực hành Toán 8. Bài viết này sẽ cung cấp đáp án và hướng dẫn giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
Cho tam giác ABC, D là một điểm nằm giữa B và C.
Đề bài
Cho tam giác ABC, D là một điểm nằm giữa B và C. Qua D kẻ các đường thẳng song song với AB, AC, chúng cắt các cạnh AC, AB lần lượt tại E, F.
a) Tứ giác AEDF là hình gì? Vì sao?
b) Nếu tam giác ABC cân tại A thì điểm D ở vị trí nào trên cạnh BC để tứ giác AEDF là hình thoi?
c) Nếu tam giác ABC vuông tại A thì tứ giác AEDF là hình gì?
d) Nếu tam giác ABC vuông cân tại A thì điểm D ở vị trí nào trên cạnh BC để AEDF là hình vuông?
Phương pháp giải - Xem chi tiết
a) Sử dụng dấu hiệu nhận biết để xác định tứ giác AEDF là hình gì.
b) Sử dụng dấu hiệu nhận biết để tứ giác AEDF là hình thoi suy ra ta có vị trí của điểm D trên cạnh BC để AEDF là hình thoi.
c) Sử dụng dấu hiệu nhận biết hình chữ nhật: Hình bình hành có một góc vuông là hình chữ nhật.
d) Sử dụng dấu hiệu nhận biết để tứ giác AEDF là hình thoi suy ra ta có vị trí của điểm D trên cạnh BC để AEDF là hình vuông.
Lời giải chi tiết
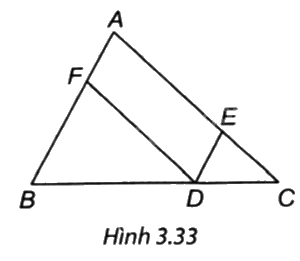
(H.3.33). a) Tứ giác AEDF có AE // DF, ED // AF nên AEDF là hình bình hành.
b) Để AEDF là hình thoi cần phải có AD là đường phân giác của góc A. Tam giác ABC cân tại A nên có đường phân giác AD cũng là đường trung tuyến, do đó D là trung điểm của BC.
Ngược lại, nếu D là trung điểm của cạnh BC thì AD cũng là đường phân giác của góc A (do tam giác ABC cân tại A). Khi đó hình bình hành AEDF có AD là đường phân giác của góc A nên nó là hình thoi.
c) Nếu tam giác ABC vuông tại A thì hình bình hành AEDF có một góc vuông nên AEDF là hình chữ nhật.
d) Nếu tam giác ABC vuông cân tại A thì AEDF là hình chữ nhật.
Để AEDF là một hình vuông thì nó còn là một hình thoi nên theo câu b, D phải là trung điểm của BC.
Bài 2 trang 61 Vở thực hành Toán 8 thuộc chương trình học Toán lớp 8, thường liên quan đến các kiến thức về hình học, cụ thể là các định lý và tính chất của hình thang cân. Việc nắm vững lý thuyết và kỹ năng giải bài tập là vô cùng quan trọng để đạt kết quả tốt trong môn học này.
Bài 2 thường yêu cầu học sinh chứng minh một tính chất nào đó của hình thang cân, hoặc tính toán các yếu tố liên quan đến hình thang cân như độ dài đường trung bình, chiều cao, góc,... Để giải bài tập này, học sinh cần:
Để giúp các em hiểu rõ hơn về cách giải bài 2 trang 61 Vở thực hành Toán 8, chúng ta sẽ cùng nhau phân tích một ví dụ cụ thể. Giả sử bài toán yêu cầu chứng minh rằng đường trung bình của hình thang cân song song với hai đáy và bằng nửa tổng hai đáy.
Vẽ hình thang cân ABCD (AB // CD), với M và N lần lượt là trung điểm của AD và BC.
Chúng ta cần chứng minh MN // AB // CD và MN = (AB + CD) / 2.
Xét tam giác ADC, M là trung điểm của AD và N là trung điểm của DC. Theo định lý đường trung bình của tam giác, ta có MN // AC và MN = AC / 2.
Tương tự, xét tam giác BCD, N là trung điểm của BC và P là trung điểm của CD. Theo định lý đường trung bình của tam giác, ta có NP // BD và NP = BD / 2.
Vì ABCD là hình thang cân nên AC = BD. Do đó, MN = NP = AC / 2 = BD / 2.
Suy ra MN = (AB + CD) / 2.
Ngoài dạng bài chứng minh tính chất của hình thang cân, bài 2 trang 61 Vở thực hành Toán 8 còn có thể xuất hiện các dạng bài tập sau:
Để giải các bài tập về hình thang cân một cách hiệu quả, các em có thể tham khảo một số mẹo sau:
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, các em có thể tự giải thêm các bài tập sau:
Hy vọng rằng với những hướng dẫn chi tiết và các mẹo giải bài tập trên, các em sẽ tự tin hơn trong việc giải bài 2 trang 61 Vở thực hành Toán 8 và các bài tập liên quan đến hình thang cân. Chúc các em học tập tốt!