Bài 5 trang 44 Vở thực hành Toán 8 tập 2 là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học về hình học, đại số để giải quyết các vấn đề thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 5 trang 44 Vở thực hành Toán 8 tập 2, giúp các em học sinh hiểu rõ bản chất của bài toán và rèn luyện kỹ năng giải toán.
Cho hàm số y = f(x) có đồ thị như hình bên.
Đề bài
Cho hàm số y = f(x) có đồ thị như hình bên.
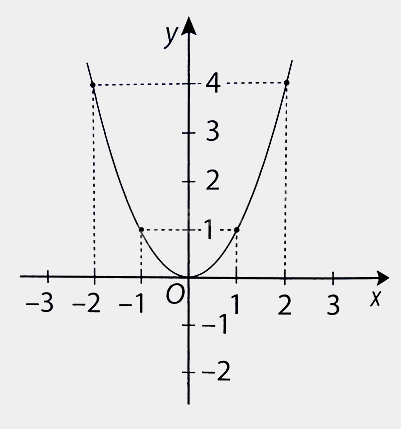
Dựa vào đồ thị hàm số hãy hoàn thành bảng giá trị của hàm số sau đây:
x | -2 | -1 | … | 1 | 2 |
y = f(x) | … | … | 0 | … | … |
Phương pháp giải - Xem chi tiết
Quan sát đồ thị để tìm các tọa độ tương ứng còn thiếu.
Lời giải chi tiết
x | -2 | -1 | 0 | 1 | 2 |
y = f(x) | 4 | 1 | 0 | 1 | 4 |
Bài 5 trang 44 Vở thực hành Toán 8 tập 2 thường thuộc các chủ đề như: tứ giác, hình bình hành, hình chữ nhật, hình thoi, hình vuông, hoặc các bài toán liên quan đến phương trình bậc nhất một ẩn. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về các loại tứ giác, các tính chất của chúng, và các phương pháp giải phương trình.
Trước khi bắt đầu giải bài toán, điều quan trọng là phải đọc kỹ đề bài, phân tích các thông tin đã cho, và xác định rõ yêu cầu của bài toán. Điều này giúp học sinh tránh được những sai sót không đáng có và tìm ra hướng giải quyết phù hợp.
(Giả sử bài toán cụ thể là: Cho hình bình hành ABCD, gọi O là giao điểm của hai đường chéo AC và BD. Chứng minh rằng OA = OC và OB = OD.)
Ngoài bài toán trên, còn rất nhiều dạng bài tập tương tự liên quan đến tứ giác và các tính chất của chúng. Để giải quyết các bài toán này, học sinh có thể áp dụng các phương pháp sau:
Để củng cố kiến thức và rèn luyện kỹ năng giải toán, học sinh có thể tự giải các bài tập sau:
Bài 5 trang 44 Vở thực hành Toán 8 tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về tứ giác và các tính chất của chúng. Hy vọng rằng với lời giải chi tiết và các phương pháp giải đã trình bày, các em học sinh sẽ hiểu rõ hơn về bài toán và tự tin giải quyết các bài tập tương tự.
| Loại tứ giác | Tính chất |
|---|---|
| Hình bình hành | Hai cạnh đối song song, hai cạnh đối bằng nhau, hai đường chéo cắt nhau tại trung điểm của mỗi đường. |
| Hình chữ nhật | Có bốn góc vuông, hai đường chéo bằng nhau, hai đường chéo cắt nhau tại trung điểm của mỗi đường. |
| Hình thoi | Bốn cạnh bằng nhau, hai đường chéo vuông góc với nhau, hai đường chéo cắt nhau tại trung điểm của mỗi đường. |
| Hình vuông | Có bốn góc vuông, bốn cạnh bằng nhau, hai đường chéo bằng nhau, hai đường chéo vuông góc với nhau, hai đường chéo cắt nhau tại trung điểm của mỗi đường. |