Bài 4 trang 84 Vở thực hành Toán 8 tập 2 là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học về hình học, đặc biệt là các định lý liên quan đến tứ giác để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4 trang 84 VTH Toán 8 tập 2, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Cho tam giác ABC cân tại đỉnh A và tam giác MNP cân tại đỉnh M. Biết rằng $widehat{BAC}=widehat{PMN}$, AB=2MN.
Đề bài
Cho tam giác ABC cân tại đỉnh A và tam giác MNP cân tại đỉnh M. Biết rằng $\widehat{BAC}=\widehat{PMN}$, AB=2MN. Chứng minh ΔMNP ∽ ΔABC và tìm tỉ số đồng dạng .
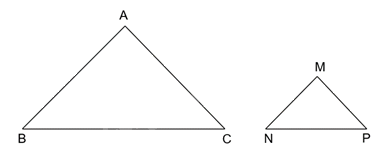
Phương pháp giải - Xem chi tiết
Sử dụng tam giác ABC cân tại A, tam giác MNP cân tại M để chứng minh ΔMNP ∽ ΔABC và tìm tỉ số đồng dạng của chúng.
Lời giải chi tiết
Vì ΔABC cân nên $\widehat{ABC}=\widehat{ACB}=\frac{\widehat{ABC}+\widehat{ACB}}{2}=\frac{{{180}^{o}}-\widehat{BAC}}{2}$ (1).
Tương tự, ΔMNP cân tại M nên $\widehat{MNP}=\frac{{{180}^{o}}-\widehat{PMN}}{2}$ (2).
Vì $\widehat{BAC}=\widehat{PMN}$ nên từ (1) và (2) ta suy ra $\widehat{ABC}=\widehat{MNP}$.
Lấy B’, C’ lần lượt là trung điểm của AB, AC thì ta có B’C’ // BC.
Do đó $\widehat{ABC}=\widehat{AB'C'},\widehat{ACB}=\widehat{AC'B'}$ (các cặp góc đồng vị).
Hai tam giác AB’C’ và MNP có:
$\widehat{BAC}=\widehat{NMP}$ (theo giả thiết),
$AB'=\frac{AB}{2}=MN$ (theo giả thiết),
$\widehat{AB'C'}=\widehat{ABC}=\widehat{MNP}$ (theo chứng minh trên).
Vậy ΔMNP = ΔAB’C’ (g.c.g). Mặt khác, ΔAB’C’ ∽ ΔABC ( vì B’C’ // BC).
Do đó ΔMNP ∽ ΔABC với tỉ số đồng dạng $k=\frac{AB'}{AB}=\frac{1}{2}$.
Bài 4 trang 84 Vở thực hành Toán 8 tập 2 thuộc chương trình học về tứ giác, một trong những kiến thức nền tảng của hình học lớp 8. Bài tập này thường yêu cầu học sinh chứng minh một tứ giác là hình gì (hình bình hành, hình chữ nhật, hình thoi, hình vuông) dựa trên các điều kiện cho trước. Để giải bài tập này hiệu quả, học sinh cần nắm vững các định nghĩa, tính chất và dấu hiệu nhận biết của các loại tứ giác đặc biệt.
Bài 4 trang 84 Vở thực hành Toán 8 tập 2 thường có dạng như sau: Cho một tứ giác ABCD, biết các yếu tố về độ dài cạnh, góc hoặc đường chéo. Yêu cầu là chứng minh tứ giác ABCD là một loại tứ giác đặc biệt nào đó.
Để giải bài tập này, học sinh có thể áp dụng các phương pháp sau:
Bài toán: Cho tứ giác ABCD có AB = CD và AD = BC. Chứng minh tứ giác ABCD là hình bình hành.
Giải:
Xét hai tam giác ABD và CDB, ta có:
Do đó, tam giác ABD bằng tam giác CDB (c-c-c). Suy ra ∠ABD = ∠CDB và ∠ADB = ∠CBD. Vì ∠ABD = ∠CDB nên AB // CD. Tương tự, vì ∠ADB = ∠CBD nên AD // BC. Vậy tứ giác ABCD là hình bình hành (dấu hiệu nhận biết hình bình hành).
Khi giải bài tập về tứ giác, học sinh cần lưu ý những điều sau:
Để rèn luyện kỹ năng giải bài tập về tứ giác, học sinh có thể làm thêm các bài tập tương tự sau:
Bài 4 trang 84 Vở thực hành Toán 8 tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về tứ giác. Bằng cách nắm vững các kiến thức nền tảng và áp dụng các phương pháp giải phù hợp, học sinh có thể giải quyết bài tập này một cách dễ dàng và hiệu quả. Giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và các hướng dẫn trên, các em học sinh sẽ học tập tốt môn Toán 8.
| Tứ giác | Định nghĩa | Tính chất |
|---|---|---|
| Hình bình hành | Tứ giác có hai cặp cạnh đối song song | Hai cạnh đối song song và bằng nhau, hai đường chéo cắt nhau tại trung điểm của mỗi đường |
| Hình chữ nhật | Hình bình hành có một góc vuông | Có bốn góc vuông, hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường |
| Hình thoi | Hình bình hành có hai cạnh kề bằng nhau | Hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường |
| Hình vuông | Hình chữ nhật có hai cạnh kề bằng nhau | Có bốn cạnh bằng nhau, bốn góc vuông, hai đường chéo bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường |