Giải bài 8 trang 54 Vở thực hành Toán 8 tập 2

Giải bài 8 trang 54 vở thực hành Toán 8 tập 2

Giải bài 8 trang 54 Vở thực hành Toán 8 tập 2

Bài 8 trang 54 Vở thực hành Toán 8 tập 2 là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học về hình học, đặc biệt là các tính chất của hình thang cân để giải quyết các bài toán thực tế.

Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 8 trang 54 Vở thực hành Toán 8 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.

Cho hàm số y = 3x + 3 (1) và y = -2x + 8 (2). a) Vẽ đồ thị hai hàm số (1) và (2) trên cùng mặt phẳng tọa độ.

Đề bài

Cho hàm số y = 3x + 3 (1) và y = -2x + 8 (2).

a) Vẽ đồ thị hai hàm số (1) và (2) trên cùng mặt phẳng tọa độ.

b) Đồ thị hai hàm số (1) và (2) cắt nhau tại A và lần lượt cắt trục hành tại B, C. Tính diện tích tam giác ABC.

Phương pháp giải - Xem chi tiết Giải bài 8 trang 54 vở thực hành Toán 8 tập 2 1

a) Lấy giao điểm của đồ thị hàm số với trục hoành và trục tung, khi đó ta được đường thẳng nối hai điểm đó là đồ thị của hàm số.

b) Tìm tọa độ giao điểm A của hai đường thẳng. Tính chiều cao và đáy của tam giác ABC để tính diện tích tam giác.

Lời giải chi tiết

a) Cho x = 0 thì y – 3, ta được giao điểm của đồ thị hàm số (1) với trục Oy là M(0; 3).

Cho y = 0 thì x = -1 , ta được giao điểm của đồ thị với trục Ox là B(-1; 0).

Vậy đồ thị hàm số (1) là đường thẳng đi qua hai điểm M(0; 3) và B(-1; 0).

Cho x = 0 thì y = 8, ta được giao điểm của đồ thị hàm số (2) với trục Oy là N(0; 8).

Cho y = 0 thì x = 4, ta được giao điểm của đồ thị với trục Ox là C(4; 0).

Vậy đồ thị hàm số (2) là đường thẳng đi qua hai điểm N(0; 8) và C(4; 0).

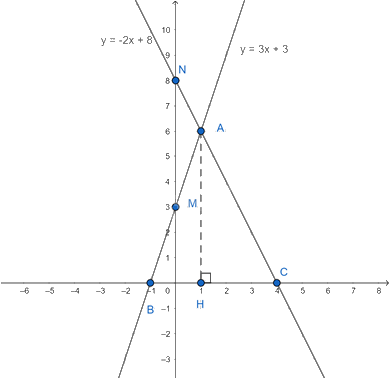
Giải bài 8 trang 54 vở thực hành Toán 8 tập 2 2

b) Dựa vào đồ thị hai hàm số (1) và (2) được vẽ ở câu a, ta suy ra tọa độ A(1; 6), B(-1; 0) và C(4; 0). Gọi H là hình chiếu vuông góc của A lên trục hoành.

Suy ra AH = |y_A| = 6 và BC = 5.

Diện tích tam giác ABC là S = $\frac{1}{2}$AH.BC = $\frac{1}{2}$.6.5 = 15.

Vững vàng kiến thức, bứt phá điểm số Toán 8! Đừng bỏ lỡ Giải bài 8 trang 54 vở thực hành Toán 8 tập 2 đặc sắc thuộc chuyên mục toán 8 trên đề thi toán. Với bộ bài tập toán trung học cơ sở được biên soạn chuyên sâu, bám sát từng chi tiết chương trình sách giáo khoa, con bạn sẽ củng cố kiến thức nền tảng vững chắc và dễ dàng chinh phục các dạng bài khó. Phương pháp học trực quan, logic sẽ giúp các em tối ưu hóa quá trình ôn luyện và đạt hiệu quả học tập tối đa!

Giải bài 8 trang 54 Vở thực hành Toán 8 tập 2: Tóm tắt lý thuyết và phương pháp giải

Bài 8 trang 54 Vở thực hành Toán 8 tập 2 thuộc chương trình học về hình thang cân. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức sau:

Định nghĩa hình thang cân: Hình thang cân là hình thang có hai cạnh bên song song.
Tính chất của hình thang cân:
- Hai góc kề một đáy bằng nhau.
- Hai đường chéo bằng nhau.
- Tổng hai góc kề một cạnh bên bằng 180 độ.
Các định lý liên quan đến đường trung bình của hình thang: Đường trung bình của hình thang song song với hai đáy và bằng nửa tổng hai đáy.

Lời giải chi tiết bài 8 trang 54 Vở thực hành Toán 8 tập 2

Để giải bài 8 trang 54 Vở thực hành Toán 8 tập 2, chúng ta cần phân tích đề bài một cách cẩn thận và xác định các yếu tố đã cho và yếu tố cần tìm. Sau đó, áp dụng các kiến thức và tính chất đã học để giải quyết bài toán.

Ví dụ: (Giả sử đề bài là: Cho hình thang cân ABCD (AB // CD), AB = 5cm, CD = 10cm, AD = 6cm. Tính chiều cao của hình thang.)

Vẽ hình: Vẽ hình thang cân ABCD với các kích thước đã cho.
Kẻ đường cao: Kẻ đường cao AH và BK từ A và B xuống CD.
Phân tích: Do ABCD là hình thang cân nên DH = KC. Ta có CD = DH + HK + KC = DH + AB + KC = 2DH + AB.
Tính toán: Từ đó suy ra DH = (CD - AB) / 2 = (10 - 5) / 2 = 2.5cm.
Áp dụng định lý Pitago: Trong tam giác vuông ADH, ta có AH² = AD² - DH² = 6² - 2.5² = 36 - 6.25 = 29.75.
Tính chiều cao: Suy ra AH = √29.75 ≈ 5.45cm. Vậy chiều cao của hình thang là 5.45cm.

Các dạng bài tập thường gặp và phương pháp giải

Ngoài bài tập tính chiều cao, bài 8 trang 54 Vở thực hành Toán 8 tập 2 và các bài tập tương tự còn có thể gặp các dạng bài sau:

Tính độ dài các cạnh của hình thang cân: Sử dụng các tính chất của hình thang cân và định lý Pitago.
Chứng minh một tứ giác là hình thang cân: Chứng minh hai cạnh bên bằng nhau hoặc hai góc kề một đáy bằng nhau.
Tính diện tích hình thang cân: Sử dụng công thức diện tích hình thang: S = (a + b)h / 2, trong đó a và b là độ dài hai đáy, h là chiều cao.

Để giải các bài tập này, học sinh cần rèn luyện kỹ năng vẽ hình, phân tích đề bài và áp dụng các kiến thức đã học một cách linh hoạt.

Bài tập luyện tập

Để củng cố kiến thức và kỹ năng giải bài tập về hình thang cân, các em học sinh có thể tự giải các bài tập sau:

Bài 9 trang 54 Vở thực hành Toán 8 tập 2
Bài 10 trang 54 Vở thực hành Toán 8 tập 2
Các bài tập tương tự trong sách giáo khoa và các tài liệu tham khảo.

Lời khuyên khi học tập

Để học tốt môn Toán 8, đặc biệt là các bài tập về hình học, các em học sinh nên:

Nắm vững các định nghĩa, tính chất và định lý.
Rèn luyện kỹ năng vẽ hình và phân tích đề bài.
Giải nhiều bài tập khác nhau để làm quen với các dạng bài và phương pháp giải.
Hỏi thầy cô giáo hoặc bạn bè khi gặp khó khăn.

Giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và các hướng dẫn trên, các em học sinh sẽ tự tin hơn khi giải bài 8 trang 54 Vở thực hành Toán 8 tập 2 và các bài tập tương tự. Chúc các em học tập tốt!