Chào mừng các em học sinh đến với lời giải chi tiết bài 5 trang 39 Vở thực hành Toán 8. Bài viết này sẽ cung cấp đáp án và hướng dẫn giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
Một mảnh vườn hình vuông có độ dài cạnh bằng x (mét).
Đề bài
Một mảnh vườn hình vuông có độ dài cạnh bằng x (mét). Người ta làm đường đi xung quanh mảnh vườn, có độ rộng như nhau và bằng y (mét) (H.2.2).
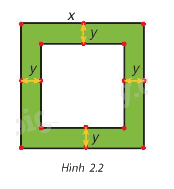
a) Viết biểu thức tính diện tích S của đường bao quanh mảnh vườn theo x và y.
b) Phân tích S thành nhân tử rồi tính S khi \(x = 102m,y = 2m\).
Phương pháp giải - Xem chi tiết
a) Viết biểu thức tính diện tích hình vuông lớn và hình vuông bé: \(S = {a^2}\) với a là độ dài cạnh hình vuông.
Diện tích S của đường bao quanh mảnh vườn = diện tích hình vuông lớn – diện tích hình vuông bé.
b) Phân tích đa thức thành nhân tử bằng cách sử dụng hằng đẳng thức hiệu hai bình phương.
Thay \(x = 102m,y = 2m\) vào đa thức để tìm S.
Lời giải chi tiết
a) Độ dài cạnh của hình vuông lớn là \(x\).
Suy ra diện tích của hình vuông lớn là \({x^2}\).
Độ dài cạnh của hình vuông bé là \(x-y\).
Suy ra diện tích của hình vuông bé là \({\left( {x-y} \right)^2}\).
Diện tích S của đường bao quanh hình vuông là
\(S = {x^2}\;-{\left( {x-y} \right)^2}\).
b) Ta có \(S = \left[ {x - \left( {x - y} \right)} \right]\left[ {x + \left( {x + y} \right)} \right]\)
\( = \left( {x - x + y} \right)\left( {x + x + y} \right) = y\left( {2x + y} \right).\)
Khi \(x = 102m,y = 2m\), ta có \(S = 2.\left( {2.102 + 2} \right) = 2.206 = 412\left( {{m^2}} \right).\)
Bài 5 trang 39 Vở thực hành Toán 8 thuộc chương trình học Toán lớp 8, thường tập trung vào các kiến thức về hình học, cụ thể là các định lý và tính chất liên quan đến hình thang cân. Việc nắm vững kiến thức nền tảng và kỹ năng giải bài tập là vô cùng quan trọng để đạt kết quả tốt trong môn học này.
Bài 5 thường bao gồm các dạng bài tập sau:
Để giải quyết bài 5 trang 39 Vở thực hành Toán 8 một cách hiệu quả, các em cần:
Bài tập: Cho hình thang cân ABCD (AB // CD), AB = 5cm, CD = 10cm, AD = 6cm. Tính độ dài BC.
Lời giải:
Vì ABCD là hình thang cân nên AD = BC. Do đó, BC = 6cm.
Dạng 1: Chứng minh một tứ giác là hình thang cân.
Để chứng minh một tứ giác là hình thang cân, ta cần chứng minh:
Dạng 2: Tính các yếu tố của hình thang cân.
Sử dụng các định lý và tính chất của hình thang cân để tính toán các yếu tố cần tìm, ví dụ như độ dài các cạnh, góc, đường cao, đường trung bình.
Các em có thể tham khảo thêm các tài liệu sau để nắm vững kiến thức về hình thang cân:
Hy vọng với những hướng dẫn chi tiết và ví dụ minh họa trên, các em học sinh đã có thể tự tin giải quyết bài 5 trang 39 Vở thực hành Toán 8 một cách hiệu quả. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!