Giải bài 8 trang 81 Vở thực hành Toán 8

Giải bài 8 trang 81 vở thực hành Toán 8

Giải bài 8 trang 81 Vở thực hành Toán 8

Chào mừng các em học sinh đến với lời giải chi tiết bài 8 trang 81 Vở thực hành Toán 8 tại giaitoan.edu.vn. Bài viết này sẽ cung cấp phương pháp giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.

Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, đồng hành cùng các em trên con đường chinh phục môn Toán.

Bác Mến muốn tính khoảng cách giữa hai vị trí P, Q ở hai bên bờ ao cá.

Đề bài

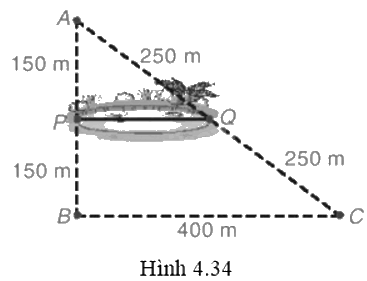
Bác Mến muốn tính khoảng cách giữa hai vị trí P, Q ở hai bên bờ ao cá. Để làm điều đó, bác Mến chọn ba vị trí A, B, C, thực hiện đo đạc và vẽ mô phỏng như Hình 4.34. Em hãy giúp bác Mến tính khoảng cách giữa hai điểm P và Q.

Giải bài 8 trang 81 vở thực hành Toán 8 1

Phương pháp giải - Xem chi tiết Giải bài 8 trang 81 vở thực hành Toán 8 2

Sử dụng tính chất đường trung bình trong tam giác.

Lời giải chi tiết

∆ABC có: P là trung điểm AB, Q là trung điểm AC nên PQ là đường trung bình của ∆ABC. Suy ra PQ // BC và PQ = \(\frac{1}{2}\)BC = 200 m.

Vững vàng kiến thức, bứt phá điểm số Toán 8! Đừng bỏ lỡ Giải bài 8 trang 81 vở thực hành Toán 8 đặc sắc thuộc chuyên mục bài tập sách giáo khoa toán 8 trên toán học. Với bộ bài tập toán trung học cơ sở được biên soạn chuyên sâu, bám sát từng chi tiết chương trình sách giáo khoa, con bạn sẽ củng cố kiến thức nền tảng vững chắc và dễ dàng chinh phục các dạng bài khó. Phương pháp học trực quan, logic sẽ giúp các em tối ưu hóa quá trình ôn luyện và đạt hiệu quả học tập tối đa!

Giải bài 8 trang 81 Vở thực hành Toán 8: Tổng quan và Phương pháp

Bài 8 trang 81 Vở thực hành Toán 8 thường thuộc các chủ đề về hình học, cụ thể là các kiến thức liên quan đến tứ giác, hình thang, hoặc các tính chất của đường trung bình trong tam giác. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các định nghĩa, định lý và tính chất cơ bản đã được học trong chương trình.

1. Tóm tắt lý thuyết cần thiết

Tứ giác: Định nghĩa, các loại tứ giác (hình chữ nhật, hình thoi, hình vuông, hình bình hành).
Hình thang: Định nghĩa, các loại hình thang (hình thang cân, hình thang vuông). Tính chất của hình thang.
Đường trung bình của tam giác: Định nghĩa, tính chất.
Các định lý về góc và cạnh trong tứ giác: Tổng các góc trong một tứ giác bằng 360 độ.

2. Phân tích bài toán và tìm hướng giải

Trước khi bắt tay vào giải bài tập, học sinh cần đọc kỹ đề bài, xác định rõ yêu cầu của bài toán. Sau đó, phân tích các dữ kiện đã cho và tìm mối liên hệ giữa chúng với các kiến thức đã học. Việc vẽ hình minh họa cũng rất quan trọng, giúp học sinh hình dung rõ hơn về bài toán và tìm ra hướng giải phù hợp.

Giải chi tiết bài 8 trang 81 Vở thực hành Toán 8

Do nội dung bài tập cụ thể không được cung cấp, chúng ta sẽ đưa ra một ví dụ minh họa về cách giải một bài tập thường gặp liên quan đến hình thang.

Ví dụ minh họa:

Cho hình thang ABCD (AB // CD). Biết AB = 5cm, CD = 10cm, AD = 6cm. Tính độ dài BC.

Hướng dẫn giải:

Kẻ đường cao AH và BK từ A và B xuống CD.
Chứng minh tam giác ADH và tam giác BCK đồng dạng.
Sử dụng tính chất của tam giác đồng dạng để tìm DH và KC.
Áp dụng định lý Pitago trong tam giác ADH và tam giác BCK để tính AH và BK.
Từ đó, tính được độ dài BC.

3. Các dạng bài tập thường gặp và phương pháp giải

Chứng minh một tứ giác là hình gì: Sử dụng các dấu hiệu nhận biết hình bình hành, hình chữ nhật, hình thoi, hình vuông.
Tính độ dài các cạnh hoặc góc trong hình thang: Sử dụng các tính chất của hình thang, đường trung bình của tam giác, định lý Pitago.
Bài tập áp dụng tính chất của đường trung bình: Sử dụng định nghĩa và tính chất của đường trung bình để giải quyết bài toán.

4. Mở rộng và nâng cao

Để nâng cao khả năng giải toán, học sinh có thể tự tìm kiếm các bài tập tương tự trên các trang web học toán online hoặc trong các sách bài tập. Đồng thời, nên tham khảo các lời giải chi tiết và phân tích của các giáo viên, chuyên gia để hiểu rõ hơn về phương pháp giải.

Luyện tập thêm

Để củng cố kiến thức và rèn luyện kỹ năng giải toán, các em có thể tham khảo thêm các bài tập sau:

Bài tập 1: Chứng minh tứ giác ABCD là hình bình hành.
Bài tập 2: Tính diện tích hình thang ABCD.
Bài tập 3: Tìm độ dài đường trung bình của tam giác ABC.

5. Lưu ý khi giải bài tập

Trong quá trình giải bài tập, học sinh cần chú ý:

Đọc kỹ đề bài và xác định rõ yêu cầu.
Vẽ hình minh họa để hình dung rõ hơn về bài toán.
Sử dụng các kiến thức đã học một cách linh hoạt và sáng tạo.
Kiểm tra lại kết quả sau khi giải xong.

Hy vọng với những hướng dẫn chi tiết trên, các em học sinh sẽ tự tin hơn trong việc giải bài 8 trang 81 Vở thực hành Toán 8 và các bài tập tương tự. Chúc các em học tập tốt!